题目内容
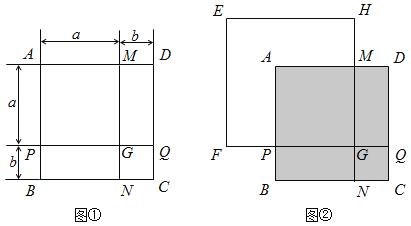
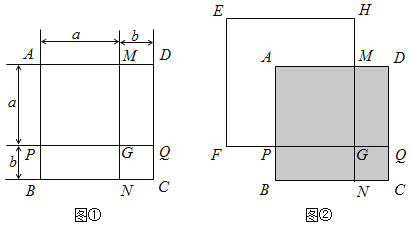
【题目】如图①,正方形ABCD是由两个长为a、宽为b的长方形和两个边长分别为a、b的正方形拼成的.
(1)利用正方形ABCD面积的不同表示方法,直接写出![]() 、
、![]() 、ab之间的关系式,这个关系式是 ;
、ab之间的关系式,这个关系式是 ;
(2)若m满足![]() ,请利用(1)中的数量关系,求
,请利用(1)中的数量关系,求![]() 的值;
的值;
(3)若将正方形EFGH的边![]() 、
、![]() 分别与图①中的PG、MG重叠,如图②所示,已知PF=8,NH=32,求图中阴影部分的面积(结果必须是一个具体数值).
分别与图①中的PG、MG重叠,如图②所示,已知PF=8,NH=32,求图中阴影部分的面积(结果必须是一个具体数值).
【答案】(1)![]() ;(2)-2019;(3)576
;(2)-2019;(3)576
【解析】
(1)由正方形ABCD的面积等于边长的平方,或者等于两个小正方形的面积+两个小长方形的面积,可得关系式;
(2)设2020﹣m=a,m﹣2019=b,由完全平方公式可求解;
(3)设正方形EFGH的边长为x,则PG=x﹣8,NG=32﹣x,由S阴=S正方形APGM+2S长方形PBNG+S正方形CQGN,代入后利用完全平方公式即可求解.
(1)根据正方形ABCD的面积等于边长的平方,即(a+b)2,也等于两个小正方形的面积+两个小长方形的面积,即a2+b2+2ab,∴(a+b)2=a2+b2+2ab.
故答案为:(a+b)2=a2+b2+2ab;
(2)设2020﹣m=a,m﹣2019=b,
则(2020﹣m)(m﹣2019)=ab,a+b=1,a2+b2=4039.
∵(a+b)2=a2+b2+2ab,∴12=4039+2ab,∴ab=﹣2019,∴(2020﹣m)(m﹣2019)=﹣2019;
(3)设正方形EFGH的边长为x,则PG=x﹣8,NG=32﹣x.
∵S阴=S正方形APGM+2S长方形PBNG+S正方形CQGN,∴![]() ,
,
∵(a+b)2=a2+b2+2ab,∴![]() 242=576.
242=576.

【题目】某水果批发市场,草莓的批发价格是每箱![]() 元,苹果的批发价格是每箱
元,苹果的批发价格是每箱![]() 元.
元.
(1)若李心批发草莓,苹果共![]() 箱,刚好花费
箱,刚好花费![]() 元,则他购买草莓、苹果各多少箱.
元,则他购买草莓、苹果各多少箱.
(2)李心有甲,乙两个店铺,每个店铺在同一时间段内都能售出草莓,苹果两种水果合计![]() 箱,并且每售出一箱草莓和苹果,甲店铺获毛利润分别为
箱,并且每售出一箱草莓和苹果,甲店铺获毛利润分别为![]() 元和
元和![]() 元,乙店铺获毛利润分别为
元,乙店铺获毛利润分别为![]() 元和
元和![]() 元.现在,李心要将批发购进的
元.现在,李心要将批发购进的![]() 箱草莓,
箱草莓,![]() 箱苹果分配给每个店铺各
箱苹果分配给每个店铺各![]() 箱.设分配给甲店草莓
箱.设分配给甲店草莓![]() 箱.
箱.
①根据信息填表:
草莓数量(箱) | 苹果数量(箱) | 合计(箱) | |
甲店 |
|
| |
乙店 |
|
②设李心获取的总毛利润为![]() 元,
元,
(1)求![]() 与
与![]() 的函数关系式:
的函数关系式:
(2)若在保证乙店铺获得毛利润不少于![]() 元的前提下,应怎样分配水果,使总毛利润
元的前提下,应怎样分配水果,使总毛利润![]() 最大,最大的总毛利润是多少元.
最大,最大的总毛利润是多少元.