题目内容
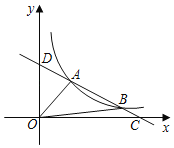
【题目】如图,在平面直角坐标系xOy中,抛物线y = ax2+ bx + c经过A、B、C三点,已知点A(-3,0),B(0,3),C(1,0).
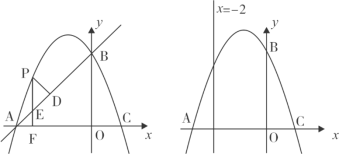
(1)求此抛物线的解析式;
(2)点P是直线AB上方的抛物线上一动点,(不与点A、B重合),过点P作x轴的垂线,垂足为F,交直线AB于点E,作PD⊥AB于点D.动点P在什么位置时,△PDE的周长最大,求出此时P点的坐标;
(3)在直线x = -2上是否存在点M,使得∠MAC = 2∠MCA,若存在,求出M点坐标.若不存在,说明理由.
【答案】(1)y=-x2-2x+3;(2)点(-![]() ,
,![]() ),△PDE的周长最大;(3)点M(-2,
),△PDE的周长最大;(3)点M(-2,![]() )或(-2,-
)或(-2,-![]() ).
).
【解析】
(1)将A、B、C三点代入,利用待定系数法求解析式;
(2)根据坐标发现,△AOB是等腰直角三角形,故只需使得PD越大,则△PDE的周长越大.联立直线AB与抛物线的解析式可得交点P坐标;
(3)作点A关于直线x=-2的对称点D,利用∠MAC = 2∠MCA可推导得MD=CD,进而求得ME的长度,从而得出M坐标
解:(1)∵抛物线y=ax2+bx+c经过点A(-3,0),B(0,3),C(1,0),
∴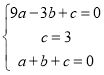 ,解得:
,解得: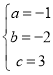 ,
,
所以,抛物线的解析式为y=-x2-2x+3;
(2)∵A(-3,0),B(0,3),
∴OA=OB=3,∴△AOB是等腰直角三角形,∴∠BAO=45°,
∵PF⊥x轴,∴∠AEF=90°-45°=45°,
又∵PD⊥AB,∴△PDE是等腰直角三角形,
∴PD越大,△PDE的周长越大,易得直线AB的解析式为y=x+3,
设与AB平行的直线解析式为y=x+m,
联立![]() ,消掉y得,x2+3x+m-3=0,
,消掉y得,x2+3x+m-3=0,
当△=9-4(m-3)=0,即m=![]() 时,直线与抛物线只有一个交点,PD最长,
时,直线与抛物线只有一个交点,PD最长,
此时x=-![]() ,y=
,y=![]() ,∴点(-
,∴点(-![]() ,
,![]() ),△PDE的周长最大;
),△PDE的周长最大;
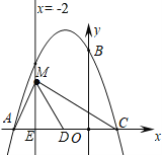
(3)设直线x=-2与x轴交于点E,作点A关于直线x=-2的对称点D,则D(-1,0),连接MA,MD,MC.
∴MA=MD,∠MAC=∠MDA=2∠MCA ,
∴∠CMD=∠DCM
∴MD=CD=2 , ∴ME=![]()
∴点M(-2,![]() )或(-2
)或(-2![]() ).
).