��Ŀ����
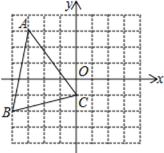
����Ŀ����֪����ͼ��ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬A��B�ֱ���y���������x���������ϵĵ㣬OA=OB=a��a�����ʽ2a��2��16=64��
��1�����A�����ꣻ
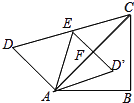
��2������C��O�������x�Ḻ���᷽���ȶ����ٶ�Ϊÿ��2����λ���ȣ�����B��BD��AC��D����y���ڵ�E����C���˶�ʱ��Ϊt���ú�t�Ĵ���ʽ��ʾ�߶�AE�ij���
��3���ڣ�2���������¹���O��OF��BD�ڵ�F����AB�ڵ�G������EG���Ƿ����tֵ��ʹ��AGE=��OGB�����������tֵ����������˵�����ɣ�
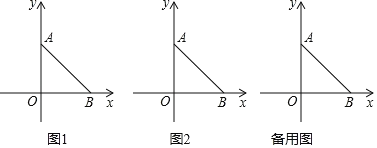
���𰸡���1��A��0��4������2��AE=4��2t����3��t=1��
��������
��1����ͬ�����ݵij˷�����a��ֵ��
��2���ɡ�AAS����֤��ACO�ա�BEO���ɵ�CO��OE��2t��������AE�ij���
��3������A��AH��OB����OG�ӳ�����H���ɡ�ASA����֤��AGE�ա�AGH���ɵ�AH��AE��4��2t���ɡ�ASA����֤��AOH�ա�OBE���ɵ�AH��OE��������t��ֵ��
��1����2a��2��16=64��
��a��2=2��
��a=4��
��OA=OB=a��
��OA=OB=4��
���A��0��4������B��4��0����
��2����ͼ1��
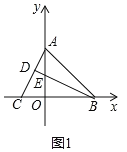
��BD��AC��AO��BC��
���ACO+��CBD=90![]() ����ACO+��CAO=90
����ACO+��CAO=90![]() ��
��
���CBD=��CAO����AO=BO����AOC=��BOE=90![]() ��
��
���ACO�ա�BEO��AAS����
��CO=OE=2t��
��AE=AO��OE=4��2t��
��3������.
��ͼ2������A��AH��OB����OG�ӳ�����H��
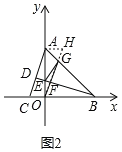
���HAO=��AOB=90![]() ��
��
��AO=BO����AOB=90![]() ��
��
���OAB=��OBA=45![]() ��
��
���HAG=��OAB=45![]() ����AG=AG����AGE=��OGB=��AGH��
����AG=AG����AGE=��OGB=��AGH��
���AGE�ա�AGH��ASA����
��AH=AE=4��2t��
��OF��BD��
���FOB+��OBD=90![]() ���ҡ�AOH+��FOB=90
���ҡ�AOH+��FOB=90![]() ��
��
���AOH=��OBD����AO=OB����HAO=��EOB��
���AOH�ա�OBE��ASA����
��AH=OE��
��4��2t=2t��
��t=1��