题目内容
【题目】青杠中学将九年级部分男生掷实心球的成绩进行整理，分成5个小组（x表示成绩，单位：米）．
组：5.25≤x＜6.25；
组：6.25≤x＜7.25；
组：7.25≤x＜8.25；
组：8.25≤x＜9.25；
组：9.25≤x＜10.25，并绘制出扇形统计图如图1和频数分布直方图（不完整）如图2．规定x≥6.25为合格，x≥9.25为优秀．
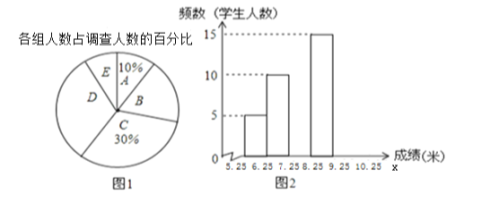
（1）这部分男生共有__________人，其中成绩合格的有___________人;
（2）这部分男生成绩的中位数落在_______组，扇形统计图中D组对应的圆心角是_____度;
（3）要从成绩优秀的学生中，随机选出2人介绍经验，已知甲、乙两位同学的成绩均为优秀，求他俩至少有1人被选中的概率．
【答案】（1）50，45；（2）C，108°；（3）
．
【解析】
试题分析：（1）根据题意可得：这部分男生共有：5÷10%=50（人）；又由只有A组男人成绩不合格，可得：合格人数为：50-5=45（人）；
（2）由这50人男生的成绩由低到高分组排序，A组有5人，B组有10人，C组有15人，D组有15人，E组有5人，可得：成绩的中位数落在C组；又由D组有15人，占15÷50=30%，即可求得：对应的圆心角为：360°×30%=108°；
（3）首先根据题意画出树状图，然后由树状图求得所有等可能的结果与他俩至少有1人被选中的情况，再利用概率公式即可求得答案．
试题解析：（1）∵A组占10%，有5人，
∴这部分男生共有：5÷10%=50（人）；
∵只有A组男人成绩不合格，
∴合格人数为：50-5=45（人）；
（2）∵C组占30%，共有人数：50×30%=15（人），B组有10人，D组有15人，
∴这50人男生的成绩由低到高分组排序，A组有5人，B组有10人，C组有15人，D组有15人，E组有5人，
∴成绩的中位数落在C组；
∵D组有15人，占15÷50=30%，
∴对应的圆心角为：360°×30%=108°；
（3）成绩优秀的男生在E组，含甲、乙两名男生，记其他三名男生为a，b，c，
画树状图得：
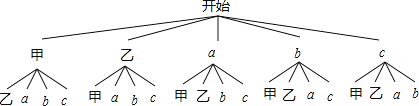
∵共有20种等可能的结果，他俩至少有1人被选中的有14种情况，
∴他俩至少有1人被选中的概率为：
．
