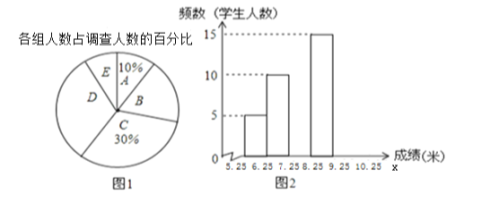
��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��A��0��1����D��-![]() ��0������ֱ��AD�����߶�ADΪһ��������������ABCD��
��0������ֱ��AD�����߶�ADΪһ��������������ABCD��
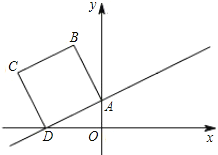
��1����գ���B������Ϊ________����C������Ϊ_________��
��2������������ÿ��2����λ���ȵ��ٶ�������DA����ƽ�ƣ�ֱ�������εĶ���C����y����ʱֹͣ�˶������˶������У�������������y���Ҳಿ�ֵ����ΪS����S����ƽ��ʱ��t���룩�ĺ�����ϵʽ����д����Ӧ���Ա���t��ȡֵ��Χ��
���𰸡���1��B�������ǣ�-1��1+![]() ����C�������ǣ�-1-
����C�������ǣ�-1-![]() ��
��![]() ������2��S=2
������2��S=2![]() t2����0��t��
t2����0��t��![]() ����S=2
����S=2![]() -4x��
-4x��![]() ��t��2����S=4-
��t��2����S=4-![]() ��3-2x��2����2��x��2+
��3-2x��2����2��x��2+![]() ����
����
��������
�����������1��BM��y���ڵ�M����CN��x���ڵ�N��֤����ABM�ա�DAO����CDN�ա�DAO������ã�
��2������֤����ADO=30��������DAO=60����Ȼ���ֻ�е�A��y���Ҳ�ʱ����B��D�ֱ�λ��y�����������ʱ����C�͵�D�ֱ�λ��y�������ʱ��������������ۣ��������Ǻ���������⣮
�����������1����BM��y���ڵ�M����CN��x���ڵ�N��
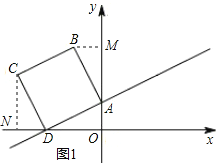
��������ABCD����BAD=90����
���BAM+��DAO=90����
����ֱ����ABM�У���BAM+��MBA=90����
���MBA=��DAO��
����ABM����DAO��
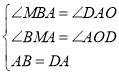 ��
��
���ABM�ա�DAO��
��BM=AO=1��AM=OD=![]() ��
��
��B�������ǣ�-1��1+![]() ����
����
ͬ������CDN�ա�DAO��
DN=AO=1��CN=OD=![]() ��
��
��C�������ǣ�-1-![]() ��
��![]() ����
����
��2����OA=1��OD=![]() ��
��
��tan��ADO=![]() ��
��
���ADO=30������DAO=60����
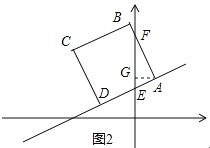
��ֻ�е�A��y���Ҳ�ʱ����ͼ2����AG��y���ڵ�G��
��ֱ����AEF�У�AE=2t����AEF=30����sin��AEG=![]() ����AG=AE
����AG=AE ![]() sin��AEG=2x
sin��AEG=2x ![]()
![]() =
=![]() x����AG=1ʱ��AE=
x����AG=1ʱ��AE=![]() ��
��
��AF=AE ![]() tan��FEA=
tan��FEA=![]() AE=2
AE=2![]() t��
t��
��S=![]() AE
AE ![]() AF=
AF=![]() ��2t��2
��2t��2![]() t=2
t=2![]() t2����0��t��
t2����0��t��![]() ����
����
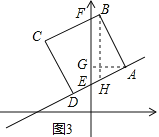
��B��D�ֱ�λ��y�����������ʱ����ͼ3����AG��y���ڵ�G����BH��y�ᣬ��AD�ڵ�H��
��ֱ����ABH�У���ABH=30������AH=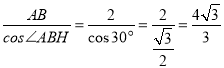 ��
��
��S=S��ABH+Sƽ���ı���BHEF=![]() AB
AB ![]() AH+BH
AH+BH ![]() ��AG-1��=
��AG-1��=![]() ��2��
��2��![]() -
-![]() ��
��![]() x-1����
x-1����
��S=2![]() -4x��
-4x��![]() ��t��2����
��t��2����
����C�͵�D�ֱ�λ��y�������ʱ����ͼ4��

ED=2x-2��
��ֱ����EDG�У�EG=![]() =4x-4����FG=2-��4x-4��=6-4x��
=4x-4����FG=2-��4x-4��=6-4x��
��ֱ����CFG�У�CF=FG ![]() sin��AGF=
sin��AGF=![]() ��6-4x��=3-2x��
��6-4x��=3-2x��
CG=![]() CF=
CF=![]() ��3-2x����
��3-2x����
��S��CFG=![]() CF
CF ![]() CG=
CG=![]() ��3-2x��2��
��3-2x��2��
��S=4-S��CFG=4-![]() ��3-2x��2����2��x��2+
��3-2x��2����2��x��2+![]() ����
����

 ��Уͨ��֤��Ч��ҵϵ�д�
��Уͨ��֤��Ч��ҵϵ�д�