题目内容
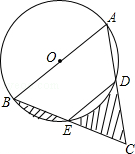
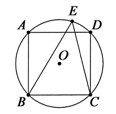
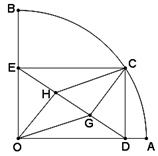
如图,AB是⊙O的直径,点E为BC的中点,AB=4,∠BED=120°,则图中阴影部分的面积之和为【 】
| A.1 | B.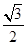 | C.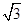 | D.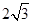 |

C。
连接AE,OD,OE。
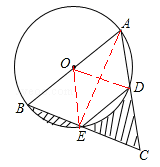
∵AB是直径, ∴∠AEB=90°。
又∵∠BED=120°,∴∠AED=30°。∴∠AOD=2∠AED=60°。
∵OA=OD。∴△AOD是等边三角形。∴∠A=60°。
又∵点E为BC的中点,∠AED=90°,∴AB=AC。
∴△ABC是等边三角形,
∴△EDC是等边三角形,且边长是△ABC边长的一半2,高是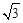 。
。
∴∠BOE=∠EOD=60°,∴ 和弦BE围成的部分的面积=
和弦BE围成的部分的面积=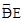 和弦DE围成的部分的面积。
和弦DE围成的部分的面积。
∴阴影部分的面积=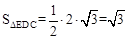 。故选C。
。故选C。

∵AB是直径, ∴∠AEB=90°。
又∵∠BED=120°,∴∠AED=30°。∴∠AOD=2∠AED=60°。
∵OA=OD。∴△AOD是等边三角形。∴∠A=60°。
又∵点E为BC的中点,∠AED=90°,∴AB=AC。
∴△ABC是等边三角形,
∴△EDC是等边三角形,且边长是△ABC边长的一半2,高是
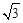 。
。∴∠BOE=∠EOD=60°,∴
 和弦BE围成的部分的面积=
和弦BE围成的部分的面积=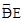 和弦DE围成的部分的面积。
和弦DE围成的部分的面积。∴阴影部分的面积=
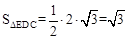 。故选C。
。故选C。
练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
 中,
中, 是它的角平分线,
是它的角平分线, ,
, 在
在 边上,
边上, 为直径的半圆
为直径的半圆 经过点
经过点 ,交
,交 于点
于点 。
。
 是
是 的切线;
的切线;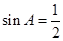 ,
,
 是定值.
是定值. 的长为【 】
的长为【 】
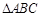 中,
中,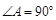 ,
, 是
是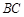 边上一点,以
边上一点,以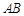 、
、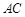 边相切于
边相切于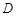 、
、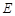 两点,连接
两点,连接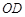 .已知
.已知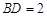 ,
,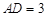 .求:
.求: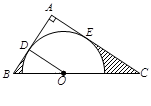
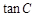 ;
;