题目内容
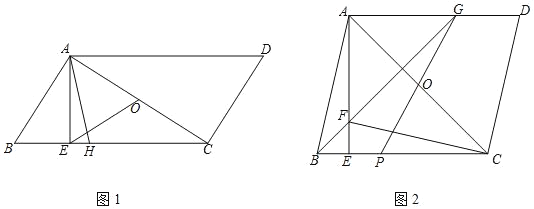
【题目】在平行四边形ABCD中,AE⊥BC于点E,AC为对角线,点O为对角线AC的中点.
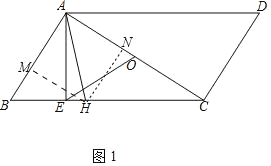
(1)如图1,若AB⊥AC,AH平分∠BAC交BC于点H,连接EO,OE=2,CD=3,求AH的长;
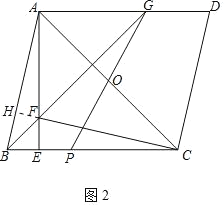
(2)如图2,若AE=EC,过C作CD的垂线交AE于点F,连接BF并延长交AD于点G,连接GO并延长GO交BC于点P,求证:DG=2EP.
【答案】(1)AH=![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)如图1中,作HM⊥AB于M,HN⊥AC于N.利用面积法求出HN,再证明△AHN是等腰直角三角形即可解决问题.
(2)如图2中,延长CF交AB于H.证明△AEB≌△CEF(ASA),推出BE=EF,证明△AOG≌△COP(ASA),推出AG=PC,再证明AG=AF=PC 推出EF=PE=BE即可解决问题.
(1)解:如图1中,作HM⊥AB于M,HN⊥AC于N.
∵AB⊥AC,
∴∠BAC=90°,
∵四边形ABCD是平行四边形,
∴AB=CD=3,
∵AE⊥BC,
∴∠AEC=90°,
∵OA=OC,OE=2,
∴AC=2OE=4,
∵AH平分∠BAC, HM⊥AB,HN⊥AC,
∴HM=HN.
∵S△ABC=![]() ABAC=
ABAC=![]() ABHM+
ABHM+![]() ACHN,
ACHN,
∴HM=HN=![]() ,
,
∵∠HAN=45°,∠ANH=90°,
∴AH=![]() HN=
HN=![]() .
.
(2)证明:如图2中,延长CF交AB于H.
∵四边形ABCD是平行四边形,
∴AB∥CD,
∵CF⊥CD,
∴CH⊥AB,
∴∠AHF=∠CEF=90°,∵∠AFH=∠CFE,
∴∠BAE=∠ECF,
∵∠AEB=∠CEF,AE=EC,
∴△AEB≌△CEF(ASA),
∴BE=EF,
∵AG∥PC,
∴∠OAG=∠OCP.
∵OA=OC,∠AOG=∠COP,
∴△AOG≌△COP(ASA),
∴AG=PC,
∵AD=BC,
∴DG=PB,
∵BE=EF,∠BEF=90°,
∴∠BEF=∠EFB=∠AFG=∠AGF=45°,
∴AG=AF,
∴AF=PC,
∵AE=EC,
∴EF=PE=BE,
∴DG=2PE.