题目内容
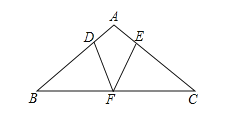
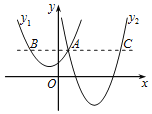
【题目】如图,抛物线y1:y=a1(x+1)2+1与y2:y=a2(x﹣4)2﹣3交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.下列结论,正确的是( )
A.![]() >
>![]() B.当
B.当![]() =
=![]() 时,x=1
时,x=1
C.当![]() >
>![]() 时,0≤x<1D.3AB=2AC
时,0≤x<1D.3AB=2AC
【答案】D
【解析】
把点A(1,3)分别代入抛物线y1:y=a1(x+1)2+1与y2:y=a2(x﹣4)2﹣3求得a1=![]() ,a2=
,a2=![]() ,得到a1<a2,故A错误,当y1=y2时,解方程得到x=1或x=37,故B错误;于是得到当y2>y1时,0≤x<1或x>37;C错误;根据抛物线的对称轴得到B(﹣3,3),C(7,3)求得AB=6,AC=4,于是得到结论.
,得到a1<a2,故A错误,当y1=y2时,解方程得到x=1或x=37,故B错误;于是得到当y2>y1时,0≤x<1或x>37;C错误;根据抛物线的对称轴得到B(﹣3,3),C(7,3)求得AB=6,AC=4,于是得到结论.
∵y=a1(x+1)2+1与y=a2(x﹣4)2﹣3交于点A(1,3),
∴3=a1(1+1)2+1,3=a2(1﹣4)2﹣3,
∴a1=![]() ,a2=
,a2=![]() ,
,
∴a1<a2,故选项A错误;
∵抛物线y1:y=a1(x+1)2+1与y2:y=a2(x﹣4)2﹣3交于点A(1,3),
∴当y1=y2时,x=1或x=37,故选项B错误;
∵当y1=y2时,x=1或x=37,
∴当y2>y1时,0≤x<1或x>37;故选项C错误;
∵抛物线y=a1(x+1)2+1与y2:y=a2(x﹣4)2﹣3交于点A(1,3),
∴y1的对称轴为x=﹣1,y2的对称轴为x=4,
∴B(﹣3,3),C(7,3)
∴AB=6,AC=4,
∴2AB=3AC,故选项D正确.
故选:D.

 计算高手系列答案
计算高手系列答案【题目】某农科所在相同条件下做某种作物种子发芽率的试验,结果如表所示:
种子个数n | 1000 | 1500 | 2500 | 4000 | 8000 | 15000 | 20000 | 30000 |
发芽种子个数m | 899 | 1365 | 2245 | 3644 | 7272 | 13680 | 18160 | 27300 |
发芽种子频率 | 0.899 | 0.910 | 0.898 | 0.911 | 0.909 | 0.912 | 0.908 | 0.910 |
则该作物种子发芽的概率约为_____________.(保留一位小数)