题目内容
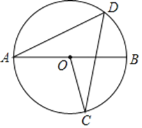
【题目】如图,已知等边△ABC中,AB=12.以AB为直径的半⊙O与边AC相交于点D.过点D作DE⊥BC,垂足为E;过点E作EF⊥AB,垂足为F,连接DF.
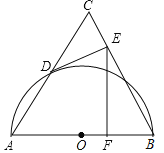
(1)求证:DE是⊙O的切线;
(2)求EF的长;
(3)求sin∠EFD的值.
【答案】(1)见解析;(2)EF=![]() ;(3)sin∠EFD=
;(3)sin∠EFD=![]() .
.
【解析】
(1)先判断出△AOD是等边三角形,进而得出OD∥BC,即可得出结论;
(2)先求出CD=6,进而求出CE,即可求出BE,即可得出结论;
(3)先求出OG,DG,再求出BF,即可求出FG,利用勾股定理求出DF,即可得出结论.
(1)如图1,连接OD,
∴∠A=∠ADO,
∵△ABC是等边三角形,
∴∠A=∠B=60°,
∴∠A=∠ADO=60°,
∴△AOD是等边三角形,
∴∠AOD=60°=∠B,
∴OD∥BC,
∵DE⊥BC,
∴DE⊥OD,
∵点D在⊙O上,
∴DE是⊙O的切线;
(2)由(1)知,OD∥BC,
∵OA=OB,
∴AD=CD,
∵AC=12,
∴CD=6,
在Rt△CDE中,∠C=60°,
∴∠CDE=30°,
∴CE=![]() CD=3,
CD=3,
∴BE=BC﹣CE=9,
在Rt△BEF中,∠B=60°,
∴∠BEF=30°,
∴EF=BEcos∠BEF=9×cos30°=![]() ;
;
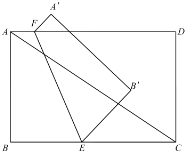
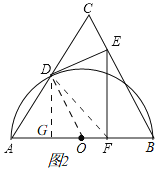
(3)如图2,连接DF,OD,过点D作DG⊥AB于G,
∵EF⊥AB,
∴∠EFD=∠GDF,
∵△AOD是等边三角形,
∴OG=![]() OA=3,
OA=3,
∴DG=OGtan∠AOD=3![]() ,
,
在Rt△BEF中,∠BEF=30°,BE=9,
∴BF=![]() BE=
BE=![]() ,
,
∴OF=OB﹣BF=6﹣![]() =
=![]()
∴FG=OG+OF=![]() ,
,
在Rt△DGF中,根据勾股定理得,DF=![]() =
=![]() ,
,
∴sin∠EFD=sin∠GDF=![]() =
=![]() =
=![]() .
.

【题目】为了了解我市中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,整理并制作出如下的统计表和统计图,如图所示,请根据图表信息解答下列问题:
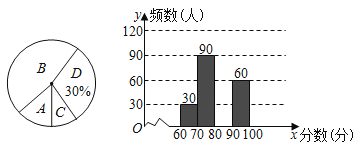
组别 | 分数段(分) | 频数 |
A组 | 60≤x<70 | 30 |
B组 | 70≤x<80 | 90 |
C组 | 80≤x<90 | m |
D组 | 90≤x<100 | 60 |
(1)本次调查的总人数为 人.
(2)补全频数分布直方图;
(3)若A组学生的平均分是65分,B组学生的平均分是75分,C组学生的平均分是85分,D出学生的平均分是95分,请你估计参加本次测试的同学们平均成绩是多少分?