题目内容
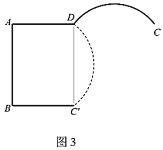
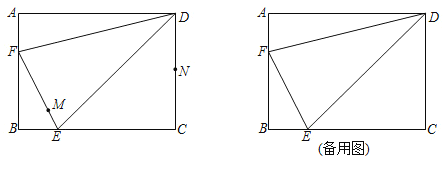
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,
上,![]() ,连接
,连接![]() ,
,![]() .动点
.动点![]() 在
在![]() 上从点
上从点![]() 向终点
向终点![]() 匀速运动,同时,动点
匀速运动,同时,动点![]() 在射线
在射线![]() .上从点
.上从点![]() 沿
沿![]() 方向匀速运动,当点
方向匀速运动,当点![]() 运动到EF的中点时,点
运动到EF的中点时,点![]() 恰好与点
恰好与点![]() 重合,点
重合,点![]() 到达终点时,
到达终点时,![]() ,
, ![]() 同时停止运动.
同时停止运动.
(1)求![]() 的长.
的长.
(2)设![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数表达式,并写出自变
的函数表达式,并写出自变![]() 的取值范围.
的取值范围.
(3)连接![]() ,当
,当![]() 与
与![]() 的一边平行时,求
的一边平行时,求![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]() (
(![]() );(3)
);(3)![]() 的值为
的值为![]() 或12
或12
【解析】
(1)由矩形的性质可得:∠B=90°,在Rt△BEF中,根据勾股定理即可求出EF的长;
(2)已知![]() ,
,![]() ,根据“当点
,根据“当点![]() 运动到EF的中点时,点
运动到EF的中点时,点![]() 恰好与点
恰好与点![]() 重合”,即可求出
重合”,即可求出![]() 关于
关于![]() 的函数表达式;
的函数表达式;
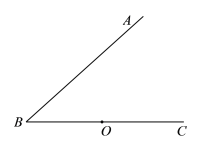
(3)如图3-1和3-2中,延长![]() 交
交![]() 的延长线于
的延长线于![]() ,根据相似三角形的判定定理可证得
,根据相似三角形的判定定理可证得![]() ,根据相似三角形对应边成比例可得EH,CH的长,然后分三种情况讨论:①
,根据相似三角形对应边成比例可得EH,CH的长,然后分三种情况讨论:①![]() ,②
,②![]() ,③
,③![]() ,排除掉不存在的情况,继而根据相似三角形对应边成比例即可求解.
,排除掉不存在的情况,继而根据相似三角形对应边成比例即可求解.
(1)∵四边形![]() 是矩形,
是矩形,
∴![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)由题意得: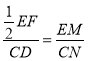 ,
,
即![]() .
.
∴![]() (
(![]() ).
).
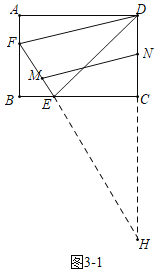
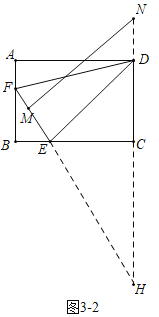
(3)如图,延长![]() 交
交![]() 的延长线于
的延长线于![]() .
.
∵四边形ABCD是矩形,
∴∠B=∠ECD=∠ECH=90°,
又∵∠BEF=∠CEH,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
①如图3-1,当![]() 时,△HMN∽△HFD,
时,△HMN∽△HFD,
∴![]() ,即
,即![]() ,
,
解得![]() ,
,
②当![]() 时,这种情形不存在.
时,这种情形不存在.
③如图3-2中,当![]() 时,△HED∽△HMN,
时,△HED∽△HMN,
∴![]() ,即
,即![]() ,
,
∵![]() ,解得
,解得![]() ,
,
综上所述,满足条件的![]() 的值为
的值为![]() 或12.
或12.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目