题目内容
【题目】如图,将一块等腰直角三角板ABC放置在平面直角坐标系中,∠ACB=90°,AC=BC,点A在y轴的正半轴上,点C在x轴的负半轴上,点B在第二象限.
(1)若AC所在直线的函数表达式是y=2x+4.
①求AC的长;
②求点B的坐标;
(2)若(1)中AC的长保持不变,点A在y轴的正半轴滑动,点C随之在x轴的负半轴上滑动.在滑动过程中,点B与原点O的最大距离是 .
【答案】
(1)
解:①当x=0时,y=2x+4=4,
∴A(0,4);
当y=2x+4=0时,x=﹣2,
∴C(﹣2,0).
∴OA=4,OC=2,
∴AC= ![]() =2
=2 ![]() .
.
②过点B作BD⊥x轴于点D,如图1所示.
∵∠ACO+∠ACB+∠BCD=180°,∠ACO+∠CAO=90°,∠ACB=90°,
∴∠CAO=∠BCD.
在△AOC和△CDB中,  ,
,
∴△AOC≌△CDB(AAS),
∴CD=AO=4,DB=OC=2,
OD=OC+CD=6,
∴点B的坐标为(﹣6,2).

(2)5+ ![]()
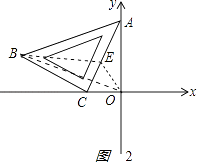
【解析】(2)如图2所示.
取AC的中点E,连接BE,OE,OB,
∵∠AOC=90°,AC=2 ![]() ,
,
∴OE=CE= ![]() AC=
AC= ![]() ,
,
∵BC⊥AC,BC=2 ![]() ,
,
∴BE= ![]() =5,
=5,
若点O,E,B不在一条直线上,则OB<OE+BE=5+ ![]() .
.
若点O,E,B在一条直线上,则OB=OE+BE=5+ ![]() ,
,
∴当O,E,B三点在一条直线上时,OB取得最大值,最大值为5+ ![]() ,
,
所以答案是:5+ ![]() .
.
【考点精析】通过灵活运用三角形三边关系和勾股定理的概念,掌握三角形两边之和大于第三边;三角形两边之差小于第三边;不符合定理的三条线段,不能组成三角形的三边;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题.

 名校课堂系列答案
名校课堂系列答案【题目】甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
根据以上信息,整理分析数据如下:
平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
甲 | a | 7 | 7 | 1.2 |
乙 | 7 | b | 8 | c |
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?





