Question

【题目】如图，在半径为6的⊙O内有两条互相垂直的弦AB和CD，AB=8，CD=6，垂足为E．则tan∠OEA的值是（ ）
A.
B.
C.
D.

Answer 1

【答案】D
【解析】解：作OM⊥AB于M，ON⊥CD于N，连接OB，OD，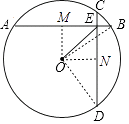
由垂径定理得：BM=AM= AB=4，DN=CN= CD=3，
由勾股定理得：OM= =2 ，ON= =3 ，
∵弦AB、CD互相垂直，OM⊥AB，ON⊥CD，
∴∠MEN=∠OME=∠ONE=90°，
∴四边形MONE是矩形，
∴ME=ON=3 ，
∴tan∠OEA= = = ，
故选D．
作OM⊥AB于M，ON⊥CD于N，连接OB，OD，根据垂径定理得出BM=AM=4，DN=CN= CD=3，根据勾股定理求出OM和ON，求出ME，解直角三角形求出即可．