Question

【题目】已知：如图，在矩形ABCD中，AB＝3，BC＝4．将△BCD沿对角线BD翻折得到△BED，BE交AD于点O．

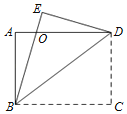
（1）判断△BOD的形状，并证明；（2）直接写出线段OD的长．

Answer 1

【答案】（1）△BOD为等腰三角形，见解析；（2）OD＝．

【解析】

（1）根据矩形的性质和翻折的性质得到∠OBD＝∠ADB，可得结论；

（2）设OD＝x，则AO＝4﹣x，BO＝OD＝x，根据勾股定理列方程可得结论．

解：（1）△BOD为等腰三角形，证明如下：

∵矩形ABCD，

∴AD∥BC．

∴∠ADB＝∠DBC．

又∵△BCD沿对角线BD翻折得到△BED，

∴∠OBD＝∠DBC．

∴∠OBD＝∠ADB．

∴OB＝OD．

∴△BOD为等腰三角形.

（2）设OD＝x，则AO＝4﹣x，BO＝OD＝x，

由勾股定理得：OB2＝AB2+AO2，

∴x2＝32+（4﹣x）2，

∴x＝，即OD＝．