题目内容
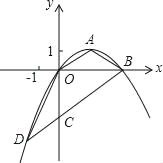
【题目】如图,顶点为A(![]() ,1)的抛物线经过坐标原点O,与x轴交于点B.
,1)的抛物线经过坐标原点O,与x轴交于点B.
(1)求抛物线对应的二次函数的表达式;
(2)过B作OA的平行线交y轴于点C,交抛物线于点D,求证:△OCD≌△OAB;
(3)在x轴上找一点P,使得△PCD的周长最小,求出P点的坐标.
【答案】(1)y=﹣![]() x2+
x2+![]() x;(2)见解析;(3)点P的坐标为(﹣
x;(2)见解析;(3)点P的坐标为(﹣![]() ,0)
,0)
【解析】试题分析:(1)用待定系数法求出抛物线解析式,(2)先求出直线OA对应的一次函数的表达式为y=![]() x.再求出直线BD的表达式为y=
x.再求出直线BD的表达式为y=![]() x﹣2.最后求出交点坐标C,D即可;
x﹣2.最后求出交点坐标C,D即可;
(3)先判断出C'D与x轴的交点即为点P,它使得△PCD的周长最小.作辅助线判断出△C'PO∽△C'DQ即可.
试题解析:解:(1)∵抛物线顶点为A(![]() ,1),设抛物线解析式为y=a(x﹣
,1),设抛物线解析式为y=a(x﹣![]() )2+1,将原点坐标(0,0)在抛物线上,∴0=a(
)2+1,将原点坐标(0,0)在抛物线上,∴0=a(![]() )2+1
)2+1
∴a=﹣![]() ,∴抛物线的表达式为:y=﹣
,∴抛物线的表达式为:y=﹣![]() x2+
x2+![]() x.
x.
(2)令y=0,得 0=﹣![]() x2+
x2+![]() x,∴x=0(舍),或x=2
x,∴x=0(舍),或x=2![]()
∴B点坐标为:(2![]() ,0),设直线OA的表达式为y=kx.∵A(
,0),设直线OA的表达式为y=kx.∵A(![]() ,1)在直线OA上,∴
,1)在直线OA上,∴![]() k=1,∴k=
k=1,∴k=![]() ,∴直线OA对应的一次函数的表达式为y=
,∴直线OA对应的一次函数的表达式为y=![]() x.
x.
∵BD∥AO,设直线BD对应的一次函数的表达式为y=![]() x+b.∵B(2
x+b.∵B(2![]() ,0)在直线BD上,∴0=
,0)在直线BD上,∴0=![]() ×2
×2![]() +b,∴b=﹣2,∴直线BD的表达式为y=
+b,∴b=﹣2,∴直线BD的表达式为y=![]() x﹣2.
x﹣2.

由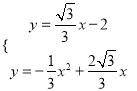
得交点D的坐标为(﹣![]() ,﹣3),令x=0得,y=﹣2,∴C点的坐标为(0,﹣2),由勾股定理,得:OA=2=OC,AB=2=CD,OB=2
,﹣3),令x=0得,y=﹣2,∴C点的坐标为(0,﹣2),由勾股定理,得:OA=2=OC,AB=2=CD,OB=2![]() =OD.
=OD.
在△OAB与△OCD中,  ,∴△OAB≌△OCD.
,∴△OAB≌△OCD.
(3)点C关于x轴的对称点C'的坐标为(0,2),∴C'D与x轴的交点即为点P,它使得△PCD的周长最小.
过点D作DQ⊥y,垂足为Q,∴PO∥DQ,∴△C'PO∽△C'DQ,∴![]() ,∴
,∴![]() ,∴PO=
,∴PO=![]() ,∴点P的坐标为(﹣
,∴点P的坐标为(﹣![]() ,0).
,0).

 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案【题目】为了鼓励市民节约用水,某市水费实行分段计费制,每户每月用水量在规定用量及以下的部分收费标准相同,超出规定用量的部分收费标准相同.例如:若规定用量为10吨,每月用水量不超过10吨按1.5元/吨收费,超出10吨的部分按2元/吨收费,则某户居民一个月用水8吨,则应缴水费:8×1.5=12(元);某户居民一个月用水13吨,则应缴水费:10×1.5+(13﹣10)×2=21(元).
表是小明家1至4月份用水量和缴纳水费情况,根据表格提供的数据,回答:
月份 | 一 | 二 | 三 | 四 |
用水量(吨) | 6 | 7 | 12 | 15 |
水费(元) | 12 | 14 | 28 | 37 |
(1)该市规定用水量为 吨,规定用量内的收费标准是 元/吨,超过部分的收费标准是 元/吨.
(2)若小明家五月份用水20吨,则应缴水费 元.
(3)若小明家六月份应缴水费46元,则六月份他们家的用水量是多少吨?