题目内容
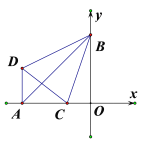
【题目】已知点![]() ,分别根据下列条件求出点P的坐标.
,分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P在y轴上;
(3)点P到x轴、y轴的距离相等;
(4)点Q的坐标为![]() ,直线
,直线![]() 轴.
轴.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;
;![]() ;(4)
;(4)![]() .
.
【解析】
(1)利用x轴上点的坐标性质纵坐标为0,进而得出a的值,即可得出答案;
(2)利用y轴上点的坐标性质横坐标为0,进而得出a的值,即可得出答案;
(3)利用点P到x轴、y轴的距离相等,得出横纵坐标相等或相反数进而得出答案;
(4)利用平行于y轴直线的性质,横坐标相等,进而得出a的值,进而得出答案;
(1)∵点P(a2,2a+8),在x轴上,
∴2a+8=0,
解得:a=4,
故a2=42=6,
则P(6,0);
(2))∵点P(a2,2a+8),在y轴上,
∴a2=0,
解得:a=2,
故2a+8=2×2+8=12,
则P(0,12);
(3)∵点P到x轴、y轴的距离相等,
∴a2=2a+8或a2+2a+8=0,
解得:a![]() =10,a
=10,a![]() =2,
=2,
故当a=10则:a2=12,2a+8=12,
则P(12,12);
故当a=2则:a2=4,2a+8=4,
则P(4,4).
综上所述:P(12,12),(4,4).
(4) ∵点Q的坐标为(1,5),直线PQ∥y轴;,
∴a2=1,
解得:a=3,
故2a+8=14,
则P(1,14);

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某校兴趣小组根据学习函数的经验,对函数![]() 的图像和性质进行探究,过程如下:
的图像和性质进行探究,过程如下:
(1)自变量x的取值范围是全体实数,x与y的几组对应值如下表:
x | ... | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | ... |
y | ... | 3 | 2.5 | m | 1.5 | 1 | 1.5 | 2 | 2.5 | 3 | ... |
其中m= .
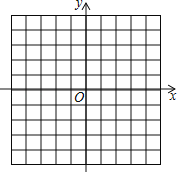
(2)如图,在平面直角坐标系xoy中,描出了上表中各对对应值为坐标的点,根据描出的点,面出该函数的图象:

(3)根据面出的函数图象特征,仿照示例,完成下列表格中的消数变化规律,
序号 | 函数图象特征 | 函数变化规律 |
示例1 | 在y轴左侧,函数图象呈下降状态 | 当x<0时,y随x的增大而减小 |
① | 在y轴右侧,函数图象呈上升状态 | |
示例2 | 函数图象经过点( -4,3) | 当x=-4时,y=3 |
② | 函数图象的最低点是(0,1) |
(4)当2<y<3时,x的取值范图为: ;