Question

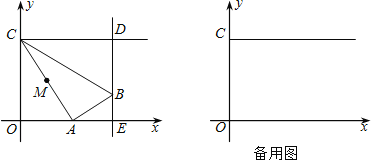
【题目】如图，在平面直角坐标系中，点C的坐标为（0，4），动点A以每秒1个单位长的速度，从点O出发沿x轴的正方向运动，M是线段AC的中点．将线段AM以点A为中心，沿顺时针方向旋转90°，得到线段AB．过点B作x轴的垂线，垂足为E，过点C作y轴的垂线，交直线BE于点D．运动时间为t秒．

（1）当点B与点D重合时，求t的值；

（2）设△BCD的面积为S，当t为何值时，S=？

（3）连接MB，当MB∥OA时，如果抛物线y=ax2﹣10ax的顶点在△ABM内部（不包括边），求a的取值范围．

Answer 1

【答案】（1）t=8（2）当t=3或3+5时，S=（3）-＜a＜-

【解析】解：（1）∵，，

∴．

∴Rt△CAO∽Rt△ABE．·························· 2分

∴．

∴．∴．························· 3分

（2）由Rt△CAO∽Rt△ABE可知：，．··········· 4分

当0＜＜8时，．

∴．····························· 6分

当＞8时，．

∴，（为负数，舍去）．

当或时，．······················ 8分

（3）过M作MN⊥轴于N，则．

当MB∥OA时，，．··············· 9分

抛物线的顶点坐标为（5，）．············· 10分

它的顶点在直线上移动．

直线交MB于点（5，2），交AB于点（5，1）．············· 11分

∴1＜＜2．

∴＜＜． 12分