Question

【题目】在Rt△ABC中，∠ACB=90°，∠A=30°，BD是△ABC的角平分线，DE⊥AB于点E．

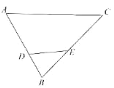
（1）如图1，连接EC，求证：△EBC是等边三角形；

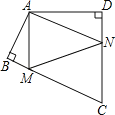
（2）点M是线段CD上的一点（不与点C，D重合），以BM为一边，在BM的下方作∠BMG=60°，MG交DE延长线于点G．请你在图2中画出完整图形，并直接写出MD，DG与AD之间的数量关系；

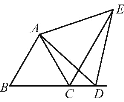
（3）如图3，点N是线段AD上的一点，以BN为一边，在BN的下方作∠BNG=60°，NG交DE延长线于点G．试探究ND，DG与AD数量之间的关系，并说明理由．

Answer 1

【答案】（1）证明见解析：（2）AD=DG+DM．（3）AD=DG-DN．理由见解析.

【解析】

（1）利用“三边相等”的三角形是等边三角形证得△EBC是等边三角形；

（2）延长ED使得DW=DM，连接MN，即可得出△WDM是等边三角形，利用△WGM≌△DBM即可得出BD=WG=DG+DM，再利用AD=BD，即可得出答案；

（3）利用等边三角形的性质得出∠H=∠2，进而得出∠DNG=∠HNB，再求出△DNG≌△HNB即可得出答案．

（1）证明：如图1所示：

在Rt△ABC中，∠ACB=90°，∠A=30°，

∴∠ABC=60°，BC=．

∵BD平分∠ABC，

∴∠1=∠DBA=∠A=30°．

∴DA=DB．

∵DE⊥AB于点E．

∴AE=BE=．

∴BC=BE．

∴△EBC是等边三角形；

（2）结论：AD=DG+DM．

证明：

如图2所示：

延长ED使得DW=DM，连接MW，

∵∠ACB=90°，∠A=30°，BD是△ABC的角平分线，DE⊥AB于点E，

∴∠ADE=∠BDE=60°，AD=BD，

又∵DM=DW，

∴△WDM是等边三角形，

∴MW=DM，

在△NGM和△DBM中，

∵

∴△WGM≌△DBM，

∴BD=WG=DG+DM，

∴AD=DG+DM．

（3）结论：AD=DG﹣DN．

证明：如图

延长BD至H，使得DH=DN．

由（1）得DA=DB，∠A=30°．

∵DE⊥AB于点E．

∴∠2=∠3=60°．

∴∠4=∠5=60°．

∴△NDH是等边三角形．

∴NH=ND，∠H=∠6=60°．

∴∠H=∠2．

∵∠BNG=60°，

∴∠BNG+∠7=∠6+∠7．

即∠DNG=∠HNB．

在△DNG和△HNB中，

∴△DNG≌△HNB（ASA）．

∴DG=HB．

∵HB=HD+DB=ND+AD，

∴DG=ND+AD．

∴AD=DG﹣ND．