题目内容
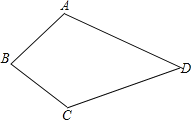
【题目】四边形ABCD中,∠BAD=125°,∠B=∠D=90°,在BC、CD上分别找一点M、N,当三角形AMN周长最小时,∠MAN的度数为_____.
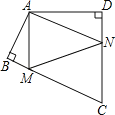
【答案】70°
【解析】
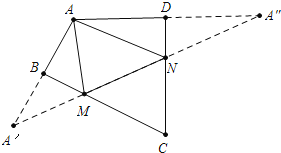
延长AB到A′使得BA′=AB,延长AD到A″使得DA″=AD,连接A′A″与BC、CD分别交于点M、N,此时△AMN周长最小,推出∠AMN+∠ANM=2(∠A′+∠A″),进而得出∠MAN的度数.
解:延长AB到A′使得BA′=AB,延长AD到A″使得DA″=AD,连接A′A″与BC、CD分别交于点M、N.
∵∠ABC=∠ADC=90°,
∴A、A′关于BC对称,A、A″关于CD对称,
此时△AMN的周长最小,
∵BA=BA′,MB⊥AB,
∴MA=MA′,同理:NA=NA″,
∴∠A′=∠MAB,∠A″=∠NAD,
∵∠AMN=∠A′+∠MAB=2∠A′,∠ANM=∠A″+∠NAD=2∠A″,
∴∠AMN+∠ANM=2(∠A′+∠A″),
∵∠BAD=125°,
∴∠A′+∠A″=180°﹣∠BAD=55°,
∴∠AMN+∠ANM=2×55°=110°.
∴∠MAN=180°﹣110°=70°,
故答案为:70°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某校1200名学生参加了一场“安全知识”问答竞赛活动,为了解笔试情况,随机抽查了部分学生的得分情况,整理并制作了如图所示的图表(部分未完成),请根据图表提供的信息,解答下列问题:
分数段 | 频数 | 频率 |
| 30 | 0.1 |
| 90 |
|
|
| 0.4 |
| 60 | 0.2 |
(Ⅰ)本次调查的样本容量为______;
(Ⅱ)在表中,![]() ______,
______,![]() ______;
______;
(Ⅲ)补全频数分布直方图;

(Ⅳ)如果比赛成绩80分以上(含80分)为优秀,本次竞赛中笔试成绩为优秀的大约有多少名学生?