题目内容
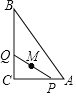
【题目】我们把满足某种条件的所有点组成的图形,叫做符合这个条件的点的轨迹,如图,在Rt△ABC中,∠C=90°,AC=8,BC=12,动点P从点A开始沿射线AC方向以1个单位秒的速度向点C运动,动点Q从点C开始沿射线CB方向以2个单位/秒的速度向点运动,P、Q两点分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,在整个运动过程中,线段PQ的中点M运动的轨迹长为__.
【答案】3![]() .
.
【解析】
先以C为原点,以AC所在直线为x轴,建立平面直角坐标系,由题意知0≤t≤6,求得t=0及t=6时M的坐标,得到直线M1M2的解析式为y=﹣2x+8.过点M2作M2N⊥x轴于点N,则M2N=6,M1N=3,M1M2=3![]() ,线段PQ中点M所经过的路径长为3
,线段PQ中点M所经过的路径长为3![]() 个单位长度.
个单位长度.
以C为原点,以AC所在直线为x轴,建立平面直角坐标系:
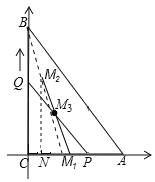
依题意,可知0≤t≤6,当t=0时,点M1的坐标为(4,0);
当t=6时,点M2的坐标为(1,6),
设直线M1M2的解析式为y=kx+b,
∴![]() ,
,
解得:![]() ,
,
∴直线M1M2的解析式为y=﹣2x+8.
设动点运动的时间为t秒,
则有点Q(0,2t),P(8﹣t,0),
∴在运动过程中,线段PQ中点M3的坐标为(![]() ,t),
,t),
把x=![]() 代入y=﹣2x+8,得y=﹣2×
代入y=﹣2x+8,得y=﹣2×![]() +8=t,
+8=t,
∴点M3在M1M2直线上,
过点M2作M2N⊥x轴于点N,则M2N=6,M1N=3,
∴M1M2=3![]() ,
,
∴线段PQ中点M所经过的路径长为3![]() 个单位长度.
个单位长度.
故答案为:3![]() .
.

练习册系列答案
相关题目