题目内容
【题目】综合与实践
折纸是同学们喜欢的手工活动之一,通过折纸我们既可以得到许多美丽的图形,同时折纸的过程还蕴含着丰富的数学知识.
折一折:把边长为4的正方形纸片![]() 对折,使边
对折,使边![]() 与
与![]() 重合,展开后得到折痕
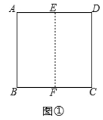
重合,展开后得到折痕![]() .如图①:
.如图①:![]() 为
为![]() 上一点,将正方形纸片
上一点,将正方形纸片![]() 沿直线
沿直线![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 的点
的点![]() 处,展开后连接
处,展开后连接![]() ,如图②
,如图②
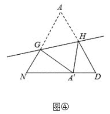
(一)做一做:
(1)图②中,求![]() 的度数和线段
的度数和线段![]() 的长度.
的长度.
(2)图②中,试判断![]() 的形状,并给出证明.
的形状,并给出证明.
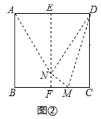
剪一剪、折一折:将图②中的![]() 剪下来,将其沿直线
剪下来,将其沿直线![]() 折叠,使点
折叠,使点![]() 落在点
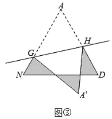
落在点![]() 处,分别得到图③、图④.
处,分别得到图③、图④.
(二)填一填:
(3)图③中阴影部分的周长为________.
(4)图③中,若![]() ,则
,则![]() __________
__________![]() .
.
(5)如图④点![]() 落在边
落在边![]() 上,若
上,若![]() ,则
,则![]() ______(用含
______(用含![]() 的代数式表示).
的代数式表示).
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 是等边三角形,理由详见解析;(3)12;(4)
是等边三角形,理由详见解析;(3)12;(4)![]() ;(5)
;(5)![]()
【解析】
(1)由折叠得四边形CDEF是矩形,ED=![]() AD=2,DN=CD=4,求出∠CDN=∠END=30°,
AD=2,DN=CD=4,求出∠CDN=∠END=30°,
由折叠得∠CDM=∠NDM得到∠CDM=15°,根据∠CMD=90°-∠CDM求出度数,根据EN=![]() ,EF=CD=4,求出NF=
,EF=CD=4,求出NF=![]() ;
;
(2)![]() 是等边三角形;由折叠得AE=DE,∠AEN=∠DEN=90°,证得
是等边三角形;由折叠得AE=DE,∠AEN=∠DEN=90°,证得![]() ,得到
,得到![]() ,再求出∠AND=90°-∠CDN=60°,即可得到△AND是等边三角形;
,再求出∠AND=90°-∠CDN=60°,即可得到△AND是等边三角形;
(3)根据等边三角形的性质得到AN=ND=AD=4,阴影部分的周长=NG+![]() +
+![]() +DH+ND=AN+AD+ND即可求出答案;
+DH+ND=AN+AD+ND即可求出答案;
(4)由![]() ,求出
,求出![]() ,利用四边形的内角和360°求出
,利用四边形的内角和360°求出![]() 再根据邻补角求出答案;
再根据邻补角求出答案;
(5)根据![]() 设
设![]() ,
,![]() (b>0),得到AN=ND=AD=b(m+n),证明△
(b>0),得到AN=ND=AD=b(m+n),证明△![]() ∽△
∽△![]() ,得到
,得到![]() =
=![]() ,即可求出答案.
,即可求出答案.
(1)由折叠得四边形CDEF是矩形,ED=![]() AD=2,DN=CD=4,
AD=2,DN=CD=4,
∵∠DEF=90°,ED=![]() DN,
DN,
∴∠END=30°,
∴∠CDN=∠END=30°,
由折叠得∠CDM=∠NDM,
∴∠CDM=15°,
∴∠CMD=90°-∠CDM=75°,
∵EN=![]() ,EF=CD=4,
,EF=CD=4,
∴NF=![]() ;
;
(2)![]() 是等边三角形;
是等边三角形;
证明:由折叠得AE=DE,∠AEN=∠DEN=90°,
又∵EN=EN,
∴![]() ,
,
∴![]() ,
,
∵∠AND=90°-∠CDN=60°,
∴△AND是等边三角形;
(3)∵△AND是等边三角形,
∴AN=ND=AD=4,
∴阴影部分的周长=NG+![]() +
+![]() +DH+ND=AN+AD+ND=12,
+DH+ND=AN+AD+ND=12,
故答案为:12;
(4)∵![]() ,
,
∴![]() ,
,
∵∠A=![]() ,
,
∴![]() ,
,
∴![]() ,
,
故答案为:![]() ;
;
(5)∵![]() ,
,
∴设![]() ,
,![]() (b>0),
(b>0),
∵△AND是等边三角形,
∴AN=ND=AD=b(m+n),
∵![]() ,
,
∴![]() ,
,
∵∠N=∠D=![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴△![]() ∽△
∽△![]() ,
,
∴![]() ,
,
=![]() .
.
∴![]()
![]() ,
,
故答案为:![]() .
.

 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案【题目】在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
销售量y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售价x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天这种水果的售价为23.5元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?