题目内容
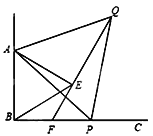
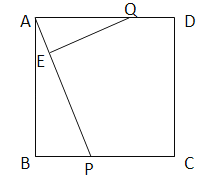
【题目】如图,正方形ABCD的边长为3 cm,P、Q分别从B、A出发沿BC,AD方向运动,P点的运动速度是1 cm/秒,Q点的运动速度是2 cm/秒。连接AP并过Q作QE⊥AP垂足为E。
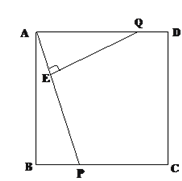
(1)求证:△ABP∽△QEA ;
(2)当运动时间t为何值时,△ABP≌△QEA;
(3)设△QEA的面积为y,用运动时间t表示△QEA的面积y。(不要求考虑t的取值范围)
(提示:解答(2)(3)时可不分先后)
【答案】(1)详见解析;(2)当t取![]() 时△ABP与△QEA全等;(3)y=
时△ABP与△QEA全等;(3)y=![]() .
.
【解析】试题分析:(1)根据正方形的性质和相似三角形的判定和性质证明即可;
(2)根据全等三角形的判定和性质,利用勾股定理解答即可;
(3)根据相似三角形的性质得出函数解析式即可.
试题解析:解:(1)∵四边形ABCD为正方形,∴∠BAP+∠QAE=∠B=90°,∵QE⊥AP,∴∠QAE+∠EQA=∠AEQ=90°,∴∠BAP=∠EQA,∠B=∠AEQ,∴△ABP∽△QEA(AA);
(2)∵△ABP≌△QEA,∴AP=AQ(全等三角形的对应边相等);
在RT△ABP与RT△QEA中根据勾股定理得: ![]() ,
, ![]() ,即
,即![]() ,解得
,解得![]() =
=![]() ,
, ![]() =﹣
=﹣![]() (不符合题意,舍去).
(不符合题意,舍去).
答:当t=![]() 时,△ABP与△QEA全等.
时,△ABP与△QEA全等.
(3)由(1)知△ABP∽△QEA,∴ 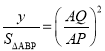 ,∴
,∴ ,整理得:
,整理得: ![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目