题目内容
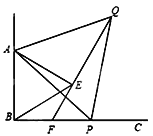
【题目】如图, 已知∠ABC=90°,点P为射线BC上任意一点(点P与点B不重合),分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ,连接QE并延长交BP于点F. 试说明:(1)△ABP≌△AEQ;(2)EF=BF
【答案】2.
【解析】(1)根据等边三角形性质得出AB=AE,AP=AQ,∠ABE=∠BAE=∠PAQ=60°,求出∠BAP=∠EAQ,根据SAS证△BAP≌△EAQ,推出∠AEQ=∠ABC=90°;
(2)根据等边三角形性质求出∠ABE=∠AEB=60°,根据∠ABC=90°=∠AEQ求出∠BEF=∠EBF=30°,即可得出答案.
(1)解:△BEC是等腰三角形,
理由是:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DEC=∠ECB,
∵CE平分∠DEB,
∴∠DEC=∠BEC,
∴∠BEC=∠ECB,
∴BE=BC,
∴△BEC是等腰三角形.
(2)解:∵四边形ABCD是矩形,
∴∠A=90°,
∵∠ABE=45°,
∴∠AEB=45°=∠ABE,
∴AE=AB=![]() ,
,
由勾股定理得:BE=![]() ,
,
即BC=BE=2.
“点睛”本题考查了等边三角形的性质,全等三角形的性质和判定,等腰三角形的性质和判定的应用.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目