题目内容
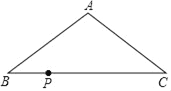
【题目】如图,在△ABC中,AB=AC=10cm,BC=16cm,现点P从点B出发,沿BC向C点运动,运动速度为![]() m/s,若点P的运动时间为t秒,则当△ABP是直角三角形时,时间t的值可能是_____.
m/s,若点P的运动时间为t秒,则当△ABP是直角三角形时,时间t的值可能是_____.
【答案】32s或50s
【解析】分析:分∠APB与∠PAB两种情况进行分类讨论,当∠APB=90°时,AP⊥BC,根据等腰三角形的性质可得出BP=CP,故可得出t的值;当∠PAB=90°时,过点A作AE⊥BC交BC于点E,由等腰三角形的性质得出BE=CE,用t表示出PE的长,再由勾股定理即可得出结论.
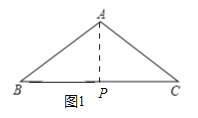
详解:如图1中,当∠APB=90°时,AP⊥BC.
∵AB=AC,AP⊥BC,∴BP=CP=![]() BC=8cm,∴
BC=8cm,∴![]() t=8,解得:t=32秒;
t=8,解得:t=32秒;
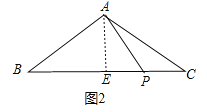
如图2中,当∠PAB=90°时,过点A作AE⊥BC交BC于点E.
∵AB=AC,AE⊥BC=8,
∴BE=CE=![]() BC=8,∴PE=BP﹣BE=
BC=8,∴PE=BP﹣BE=![]() t﹣8.
t﹣8.
在Rt△AEC中,AE2=AC2﹣CE2,即AE2=102﹣82,解得:AE=6cm.
在Rt△PAB中,AP2=BP2﹣AB2.在Rt△AEP中,AE2=PE2+AE2,∴(![]() t)2﹣100=(
t)2﹣100=(![]() t﹣8)2+36,解得:t=50(秒).
t﹣8)2+36,解得:t=50(秒).
综上所述:t的值为32秒或50秒.
故答案为:32s或50s.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目