题目内容
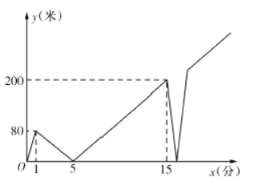
【题目】一天清晨,甲、乙两人在一条笔直的道路上同起点、同终点往返跑步.甲跑了![]() 分钟后乙再出发,当乙追上甲时,甲加快速度往前跑,先到达终点后立刻以加快后的速度返回起点.已知甲加速前、后分别保持匀速跑,乙全程均保持匀速跑下图是甲乙两人之间的距离
分钟后乙再出发,当乙追上甲时,甲加快速度往前跑,先到达终点后立刻以加快后的速度返回起点.已知甲加速前、后分别保持匀速跑,乙全程均保持匀速跑下图是甲乙两人之间的距离![]() (米)与甲跑步的时间
(米)与甲跑步的时间![]() (分)的部分函数图象.则当乙第一次到达终点时,甲距起点______米.
(分)的部分函数图象.则当乙第一次到达终点时,甲距起点______米.
【答案】![]()
【解析】
先根据题意得到甲开始1分钟跑80米,甲跑5分钟被乙追上;甲15分钟跑到终点,此时与乙相距200米,然后利用行程问题的关系解答即可.
解:由函数图象可知:甲开始1分钟跑80米,甲跑1分钟后乙出发,4分钟被乙追上;甲15分钟跑到终点,此时与乙相距200米,
∵甲开始1分钟跑80米,甲跑1分钟后乙出发,甲跑5分钟被乙追上;;
∴乙跑步的速度为![]() 100(米/分),
100(米/分),
∴起点与终点的距离为100×(15-1)+200=1600(米),
∴甲加速后的速度为![]() (米/分),
(米/分),
∴当乙第一次到达终点时,甲距起点2×1600-80×5-120×![]() =1360(米)
=1360(米)
故答案为1360.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目