题目内容
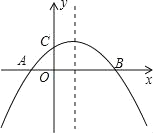
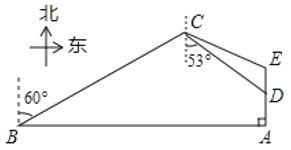
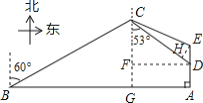
【题目】如图，我南海某海域A处有一艘捕鱼船在作业时突遇特大风浪，船长马上向我国渔政搜救中心发出求救信号，此时一艘渔政船正巡航到捕鱼船正西方向的B处，该渔政船收到渔政求救中心指令后前去救援，但两船之间有大片暗礁，无法直线到达，于是决定马上调整方向，先向北偏东60°方向以每小时40海里的速度航行半小时到达C处，同时捕鱼船低速航行到A点的正北2海里D处，渔政船航行到点C处时测得点D在南偏东53°方向上．
（1）求CD两点的距离；
（2）渔政船决定再次调整航向前去救援，若两船航速不变，并且在点E处相会合，求∠ECD的正弦值．（参考数据：
，
，
，
）
【答案】（1）
；（2）0.08
【解析】
（1）过点
、
分别作
，
，垂足分别为
，
，根据直角三角形的性质得出
，再根据三角函数的定义即可得出
的长；
（2）如图，设渔政船调整方向后
小时能与捕渔船相会合，由题意知
，
，
，过点
作
于点
，根据三角函数表示出
，在
中，根据正弦的定义求值即可．
解：（1）过点、分别作，，垂足分别为，，
在
中，
，
，
，
∴四边形
是矩形，
，
，
在
中，
，
，
，
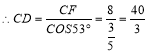（海里）．
答：两点的距离是；
（2）如图，设渔政船调整方向后小时能与捕渔船相会合，
由题意知，，，
过点作于点，则
，
，
，
在中，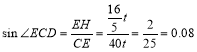
．
答：
．
练习册系列答案
相关题目
【题目】某水产养殖户进行小龙虾养殖. 已知每千克小龙虾养殖成本为6元，在整个销售旺季的80天里，日销售量
与时间第
天之间的函数关系式为
（
，为整数），销售单价
（元/
）与时间第天之间满足一次函数关系如下表：
时间第 | 1 | 2 | 3 | … | 80 |
销售单价 | 49. 5 | 49 | 48. 5 | … | 10 |
（1）写出销售单价（元/）与时间第天之间的函数关系式；
（2）在整个销售旺季的80天里，哪一天的日销售利润最大？最大利润是多少？
