题目内容
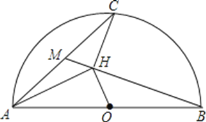
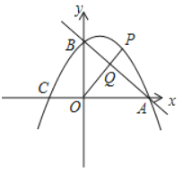
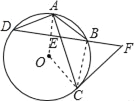
【题目】如图所示,⊙O中,弦AC、BD交于E,![]() .
.
(1)求证:![]() ;
;
(2)延长EB到F,使EF=CF,试判断CF与⊙O的位置关系,并说明理由.
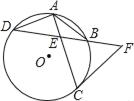
【答案】(1)详见解析;(2)CF与⊙O相切,理由详见解析.
【解析】
(1)连接BC,由![]() =2
=2![]() ,得
,得![]() =
=![]() ,则∠ABD=∠ACB,得到△ABE∽△ABC,所以AB2=AEAC;
,则∠ABD=∠ACB,得到△ABE∽△ABC,所以AB2=AEAC;
(2)连接AO、CO,由A为![]() 中点,得到AO⊥DB,得到∠OAC+∠AED=90°,所以∠OAC+∠FEC=90°,而EF=CF,则∠FEC=∠ECF,又∠OAC=∠OCA,所以∠OAC+∠FEC=∠OCA+∠ECF=90°,即得到CF与⊙O相切.
中点,得到AO⊥DB,得到∠OAC+∠AED=90°,所以∠OAC+∠FEC=90°,而EF=CF,则∠FEC=∠ECF,又∠OAC=∠OCA,所以∠OAC+∠FEC=∠OCA+∠ECF=90°,即得到CF与⊙O相切.
证明:(1)连接BC,如图,
∵![]() =2
=2![]() .
.
∴![]() =
=![]() .
.
∴∠ABD=∠ACB,
而∠CAB公用,
∴△ABE∽△ABC,
∴![]()
∴![]()
(2)CF与⊙O相切.理由如下:
连接AO、CO,
∵A为![]() 中点,
中点,
∴AO⊥DB,
∴∠OAC+∠AED=90°
∵∠AED=∠FEC,
∴∠OAC+∠FEC=90°,
又∵EF=CF,
∴∠FEC=∠ECF,
∵AO=OC,
∴∠OAC=∠OCA,
∴∠OAC+∠FEC=∠OCA+∠ECF=90°,
∴FC与⊙O相切.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目