题目内容
【题目】某商场第一次购进20件A商品,40件B商品,共用了1980元.脱销后,在进价不变的情况下,第二次购进40件A商品,20件B商品,共用了1560元.商品A的售价为每件30元,商品B的售价为每件60元.
(1)求A,B两种商品每件的进价分别是多少元?
(2)为了满足市场需求,需购进A,B两种商品共1000件,且A种商品的数量不少于B种商品数量的3倍,请你设计进货方案,使这1000件商品售完后,商场获利最大,并求出最大利润.
【答案】(1)A种商品每件的进价为19元,B种商品每件的进价为40元;(2)当购进A种商品750件、B种商品250件时,销售利润最大,最大利润为13250元.
【解析】
(1)设A种商品每件的进价为x元,B种商品每件的进价为y元,根据两次进货情况表,可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)设购进B种商品m件,获得的利润为w元,则购进A种商品(1000-m)件,根据总利润=单件利润×购进数量,即可得出w与m之间的函数关系式,由A种商品的数量不少于B种商品数量的3倍,即可得出关于m的一元一次不等式,解之即可得出m的取值范围,再根据一次函数的性质即可解决最值问题.
(1)设A种商品每件的进价为x元,B种商品每件的进价为y元,
根据题意得:![]() ,
,
解得:![]() .
.
答:A种商品每件的进价为19元,B种商品每件的进价为40元;
(2)设购进B种商品m件,获得的利润为w元,则购进A种商品(1000﹣m)件,
根据题意得:w=(30﹣19)(1000﹣m)+(60﹣40)m=9m+11000.
∵A种商品的数量不少于B种商品数量的3倍,
∴![]() ,
,
解得:![]() ,
,
∵在w=9m+11000中,k=9>0,
∴w的值随m的增大而增大,
∴当m=250时,w取最大值,最大值为9×250+11000=13250,
∴当购进A种商品750件、B种商品250件时,销售利润最大,最大利润为13250元.

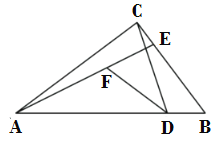
【题目】如图,在平行四边形ABCD中,M、N分别是边AD、BC边上的中点,且△ABM≌△DCM;E、F分别是线段BM、CM的中点.
(1)求证:平行四边形ABCD是矩形.
(2)求证:EF与MN互相垂直.

【题目】某班“数学兴趣小组”对函数![]() ,的图象和性质进行了探究过程如下,请补充完成:
,的图象和性质进行了探究过程如下,请补充完成:
(1)函数![]() 的自变量
的自变量![]() 的取值范围是__________________;
的取值范围是__________________;
(2)下表是![]() 与
与![]() 的几组对应值.请直接写出
的几组对应值.请直接写出![]() ,
,![]() 的值:
的值:![]() ______________;
______________;![]() ________.
________.
| … |
|
| 0 |
|
|
|
| 2 | 3 | 4 | … |
| … |
|
|
|
| -3 | 5 | 3 |
|
| … |
(3)如图,在平面直角坐标系![]() 中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
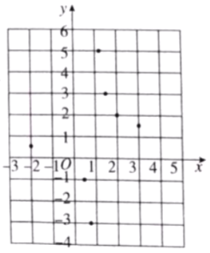
(4)通过观察函数的图象,小明发现该函数图象与反比例函数![]() 的图象形状相同,是中心对称图形,且点
的图象形状相同,是中心对称图形,且点![]() 和
和![]() 是一组对称点,则其对称中心的坐标为________.
是一组对称点,则其对称中心的坐标为________.
(5)请写出一条该函数的性质:___________________.
(6)当![]() 时,关于
时,关于![]() 的方程
的方程![]() 有实数解,求
有实数解,求![]() 的取值范围.
的取值范围.
【题目】某市少年宫为小学生开设了绘画、音乐、舞蹈和跆拳道四类兴趣班,为了解学生对这四类兴趣班的喜爱情况,对学生进行了随机问卷调查(问卷调查表如图所示),将调查结果整理后绘制了一幅不完整的统计表
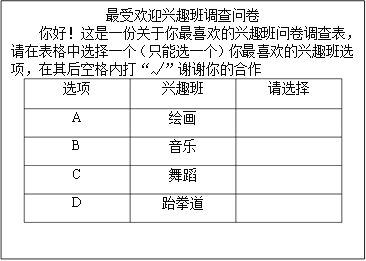
兴趣班 | 频数 | 频率 |
A | 0.35 | |
B | 18 | 0.30 |
C | 15 |
|
D | 6 | |
合计 |
| 1 |
请你根据统计表中提供的信息回答下列问题:
(1)统计表中的![]() ,
,![]() ;
;
(2)根据调查结果,请你估计该市2000名小学生中最喜欢“绘画”兴趣的人数;
(3)王姝和李要选择参加兴趣班,若他们每人从![]() 、
、![]() 、
、![]() 、
、![]() 四类兴趣班中随机选取一类,请用画树状图或列表格的方法,求两人恰好选中同一类的概率.
四类兴趣班中随机选取一类,请用画树状图或列表格的方法,求两人恰好选中同一类的概率.