题目内容
【题目】在平面直角坐标系中,我们不妨把横坐标和纵坐标相等的点叫“相等点”,例如点![]() ,
,![]()
![]() 都是“相等点”,显然“相等点”有无数个.
都是“相等点”,显然“相等点”有无数个.
(1)若点![]() 是反比例函数
是反比例函数![]() 为常数,
为常数,![]() )的图象上的“相等点”,求这个反比例函数的解析式;
)的图象上的“相等点”,求这个反比例函数的解析式;
(2)一次函数![]() 为常数,
为常数,![]() )的图象上存在“相等点”吗?若存在,请用含
)的图象上存在“相等点”吗?若存在,请用含![]() 的式子表示出“相等点”的坐标,若不存在,说明理由;
的式子表示出“相等点”的坐标,若不存在,说明理由;
(3)若二次函数![]() 为常数)的图象上有且只有一个“相等点”,令
为常数)的图象上有且只有一个“相等点”,令![]() 当
当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)当
;(2)当![]() 时不存在,当
时不存在,当![]() 时存在.理由见解析;当
时存在.理由见解析;当![]() 时,函数
时,函数![]() 的图象上的“相等点”是
的图象上的“相等点”是![]() ;(3)
;(3)![]() 的取值范围是
的取值范围是![]() .
.
【解析】
(1)根据相等点的定义求得![]() 的值,再用待定系数法求得解析式;
的值,再用待定系数法求得解析式;
(2)设![]() 是一次函数
是一次函数![]() 为常数,
为常数,![]() 的图象上的“相等点”,代入解析式求得
的图象上的“相等点”,代入解析式求得![]() 便可;
便可;
(3)若二次函数![]() ,
,![]() 为常数)的图象上有且只有一个“相等点”,则二次函数
为常数)的图象上有且只有一个“相等点”,则二次函数![]() 与直线
与直线![]() 有且只有一个交点,由此得一元二次方程
有且只有一个交点,由此得一元二次方程![]() 的有且只有2个相等的实数根,由此列出
的有且只有2个相等的实数根,由此列出![]() 和
和![]() 的关系式,进而根据
的关系式,进而根据![]() 的取值范围求得
的取值范围求得![]() 的取值范围,再求
的取值范围,再求![]() 的取值范围便可.
的取值范围便可.
解:(1)![]() 点
点![]() 是反比例函数
是反比例函数![]() 为常数,
为常数,![]() 的图象上的“相等点”,
的图象上的“相等点”,
![]() ,
,
![]() ,
,
把![]() 代入
代入![]() 中,得
中,得![]() ,
,
![]() 反比例的解析式为
反比例的解析式为![]() ;
;
(2)![]() 设
设![]() 是一次函数
是一次函数![]() 为常数,
为常数,![]() 的图象上的“相等点”,则
的图象上的“相等点”,则
![]() ,
,
![]() ,
,
当![]() ,即
,即![]() 时,方程无解,则此时一次函数
时,方程无解,则此时一次函数![]() 为常数,
为常数,![]() 的图象上不存在“相等点”,
的图象上不存在“相等点”,
当![]() ,即
,即![]() 时,得
时,得![]() ,则此时一次函数
,则此时一次函数![]() 为常数,
为常数,![]() 的图象上的“相等点”是
的图象上的“相等点”是![]() ,
,![]() ,
,
故当![]() 时,一次函数
时,一次函数![]() 为常数,
为常数,![]() 的图象上不存在“相等点”;当
的图象上不存在“相等点”;当![]() 时,一次函数
时,一次函数![]() 为常数,
为常数,![]() 的图象上的“相等点”是
的图象上的“相等点”是![]() ,
,![]() .
.
(3)![]() 二次函数
二次函数![]() ,
,![]() 为常数)的图象上有且只有一个“相等点”,
为常数)的图象上有且只有一个“相等点”,
![]()
![]() 只有一个解,
只有一个解,
![]() ,即
,即![]() 有两个相等的实数根,
有两个相等的实数根,
![]() △
△![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() .
.

【题目】2018年平昌冬奥会在2月9日到25日在韩国平昌郡举行,为了调查中学生对冬奥会比赛项目的了解程度,某中学在学生中做了一次抽样调查,调查结果共分为四个等级:A、非常了解B、比较了解C、基本了解D、不了解.根据调查统计结果,绘制了如图所示的不完整的三种统计图表.
对冬奥会了解程度的统计表
对冬奥会的了解程度 | 百分比 |
A非常了解 | 10% |
B比较了解 | 15% |
C基本了解 | 35% |
D不了解 | n% |
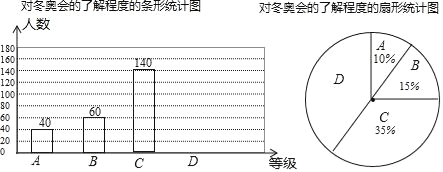
(1)n= ;
(2)扇形统计图中,D部分扇形所对应的圆心角是 ;
(3)请补全条形统计图;
(4)根据调查结果,学校准备开展冬奥会的知识竞赛,某班要从“非常了解”程度的小明和小刚中选一人参加,现设计了如下游戏来确定谁参赛,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4然后放到一个不透明的袋中,一个人先从袋中摸出一个球,另一人再从剩下的三个球中随机摸出一个球,若摸出的两个球上的数字和为偶数,则小明去,否则小刚去,请用画树状图或列表的方法说明这个游戏是否公平.