题目内容
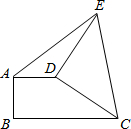 如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,将腰CD以D为中心逆时针旋转90°至DE,连接AE、CE.若S△ADE=3,CE=
如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,将腰CD以D为中心逆时针旋转90°至DE,连接AE、CE.若S△ADE=3,CE=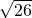 ,则梯形ABCD的面积是________.
,则梯形ABCD的面积是________.
7
分析:先过D点作DF⊥BC,垂足为F,过E点作EG⊥AD,交AD的延长线与G点,由旋转的性质可知△CDF≌△EDG,从而有CF=EG,由△ADE的面积可求EG,得出CF的长,由矩形的性质得BF=AD,从而求出BC的长,再根据∠CDE=90°,得出CD2+DE2=CE2,求出CD的长,最后根据勾股定理求出DF的值,即可求出梯形ABCD的面积.
解答: 解:过D点作DF⊥BC,垂足为F,过E点作EG⊥AD,交AD的延长线与G点,
解:过D点作DF⊥BC,垂足为F,过E点作EG⊥AD,交AD的延长线与G点,
由旋转的性质可得:CD=ED,∠EDG+∠CDG=∠CDG+∠FDC=90°,
在△CDF和△EDG中,
∵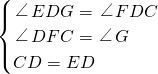 ,
,
∴△CDF≌△EDG,
∴CF=EG,CD=DE,
∵S△ADE= AD×EG=3,AD=2,
AD×EG=3,AD=2,
∴EG=3,则CF=EG=3,
∵四边形ABFD为矩形,
∴BF=AD=2,
∴BC=BF+CF=2+3=5,
∵∠CDE=90°,
∴CD2+DE2=CE2,
∴2CD2=CE2,
∴2CD2=(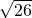 )2,
)2,
∴CD= ,
,
∴DF= =
= =2,
=2,
∴梯形ABCD的面积是: (AD+BC)•DF=
(AD+BC)•DF= (2+5)×2=7;
(2+5)×2=7;
故答案为:7.
点评:本题考查了直角梯形、全等三角形的判定与性质、勾股定理和旋转的性质,解题的关键是通过DC、DE的旋转关系,作出旋转的三角形,再根据旋转的性质求出各边的长.
分析:先过D点作DF⊥BC,垂足为F,过E点作EG⊥AD,交AD的延长线与G点,由旋转的性质可知△CDF≌△EDG,从而有CF=EG,由△ADE的面积可求EG,得出CF的长,由矩形的性质得BF=AD,从而求出BC的长,再根据∠CDE=90°,得出CD2+DE2=CE2,求出CD的长,最后根据勾股定理求出DF的值,即可求出梯形ABCD的面积.
解答:
 解:过D点作DF⊥BC,垂足为F,过E点作EG⊥AD,交AD的延长线与G点,
解:过D点作DF⊥BC,垂足为F,过E点作EG⊥AD,交AD的延长线与G点,由旋转的性质可得:CD=ED,∠EDG+∠CDG=∠CDG+∠FDC=90°,
在△CDF和△EDG中,
∵
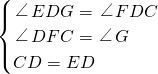 ,
,∴△CDF≌△EDG,
∴CF=EG,CD=DE,
∵S△ADE=
 AD×EG=3,AD=2,
AD×EG=3,AD=2,∴EG=3,则CF=EG=3,
∵四边形ABFD为矩形,
∴BF=AD=2,
∴BC=BF+CF=2+3=5,
∵∠CDE=90°,
∴CD2+DE2=CE2,
∴2CD2=CE2,
∴2CD2=(
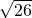 )2,
)2,∴CD=
 ,
,∴DF=
 =
= =2,
=2,∴梯形ABCD的面积是:
 (AD+BC)•DF=
(AD+BC)•DF= (2+5)×2=7;
(2+5)×2=7;故答案为:7.
点评:本题考查了直角梯形、全等三角形的判定与性质、勾股定理和旋转的性质,解题的关键是通过DC、DE的旋转关系,作出旋转的三角形,再根据旋转的性质求出各边的长.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
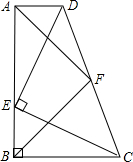 如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,点E是AB边上一点,AE=BC,DE⊥EC,取DC的中点F,连接AF、BF.
如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,点E是AB边上一点,AE=BC,DE⊥EC,取DC的中点F,连接AF、BF.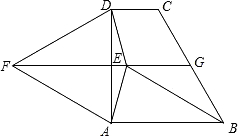 ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.
ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.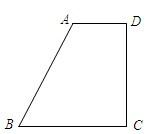 如图,直角梯形ABCD中,AD∥BC,∠BCD=90°,且CD=2AD,tan∠ABC=2.
如图,直角梯形ABCD中,AD∥BC,∠BCD=90°,且CD=2AD,tan∠ABC=2.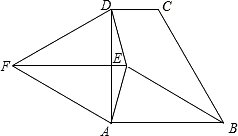 (2013•深圳二模)如图,直角梯形ABCD中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60°.以AD为边在直角梯形ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.
(2013•深圳二模)如图,直角梯形ABCD中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60°.以AD为边在直角梯形ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF. 已知:如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,以AB为直径的⊙O切DC边于E点,AD=3cm,BC=5cm.求⊙O的面积.
已知:如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,以AB为直径的⊙O切DC边于E点,AD=3cm,BC=5cm.求⊙O的面积.