题目内容
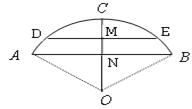
【题目】一跨河桥,桥拱是圆弧形,跨度(AB)为12米,拱高(CN)为2米,求:
(1)桥拱半径;
(2)大雨过后,桥下河面宽度(DE)为10米,求水面涨高了多少?
【答案】(1)r=10m;(2) ![]()
【解析】试题分析:(1)利用直角三角形,根据勾股定理和垂径定理解答.(2)已知到桥下水面宽AB为12m,即是已知圆的弦长,已知桥拱最高处离水面2m,就是已知弦心距,可以利用垂径定理转化为解直角三角形的问题.
试题解析:
(1)∵拱桥的跨度AB=12m,拱高CN=2m,
∴AN=6m,
利用勾股定理可得:
AO2(OCCN)2=6×6,
解得OA=10,
答:桥拱半径为10米.
(2)设河水上涨到DE位置,
这时DE=10m,DE∥AB,有OC⊥DE(垂足为M),
∴EM=![]() EF=5m,
EF=5m,
连接OE,则有OE=10m,
OM=![]() =5
=5![]() (m)
(m)
MC=OCOM=105![]() (m),
(m),
NCCM=2(105![]() )=5
)=5![]() 8(m).
8(m).
答:水面涨高了5![]() 8米.
8米.

练习册系列答案
相关题目