题目内容
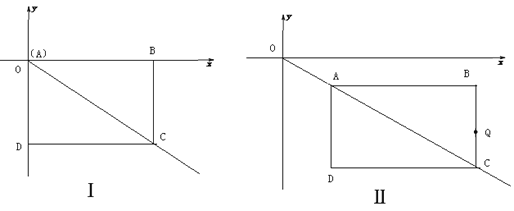
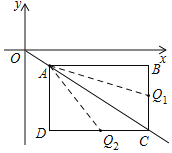
【题目】如图Ⅰ,在第四象限的矩形ABCD,点A与坐标原点O重合,且AB=4,AD=3.如图Ⅱ,矩形ABCD沿OC方向以每秒1个单位长度的速度运动,同时点Q从B点出发也以每秒1个单位长度的速度沿矩形ABCD的边BC经过点C向点D运动,当点Q到达点D时,矩形ABCD和点Q同时停止运动,设点Q运动的时间为t秒.
(1)在图Ⅰ中,点C的坐标(____),在图Ⅱ中,当t=2时,点A坐标(______),Q坐标(______)
(2)当点Q在线段BC或线段CD上运动时,求出△ACQ的面积S关于t的函数关系式,并写出t的取值范围;
(3)点Q在线段BC或线段CD上运动时,作QM⊥x轴,垂足为点M,当△QMO与△ACD相似时,求出相应的t值.
【答案】(1)C(4,-3); A(![]() ), Q(
), Q(![]() );
);
(2)①当Q在BC上,即0≤t≤3时,S=6-2t,②当Q在CD上,即3<t≤7时,S=![]() ;
;
(3)当t=3时,△QMO与△ACD相似.
【解析】试题分析:(1)根据AB=4,AD=3,可得点A的坐标,过A作AE⊥x轴于E,根据△AOE∽△CAB,可得AE:OE:AO=3:4:5,再根据当t=2时,OA=2,OE=![]() ,AE=
,AE=![]() ,BQ=2,可得点A和点Q的坐标;(2)分两种情况进行讨论:①当点Q在BC上时,②当点Q在CD上时,分别根据△ACQ的面积计算方法,求得S关于t的函数关系式,并根据点Q的位置写出t的取值范围;(3)先过A作AE⊥x轴于E,根据△AOE∽△CAB,得出AE:OE:AO=3:4:5,再根据OA=t,得出OE=
,BQ=2,可得点A和点Q的坐标;(2)分两种情况进行讨论:①当点Q在BC上时,②当点Q在CD上时,分别根据△ACQ的面积计算方法,求得S关于t的函数关系式,并根据点Q的位置写出t的取值范围;(3)先过A作AE⊥x轴于E,根据△AOE∽△CAB,得出AE:OE:AO=3:4:5,再根据OA=t,得出OE=![]() t,AE=
t,AE=![]() t,再分两种情况进行讨论:①当点Q在BC上时,连接OQ,②当点Q在CD上时,连接OQ,分别根据相似三角形的对应边成比例,列出关于t的比例式,求得t的值并检验即可.
t,再分两种情况进行讨论:①当点Q在BC上时,连接OQ,②当点Q在CD上时,连接OQ,分别根据相似三角形的对应边成比例,列出关于t的比例式,求得t的值并检验即可.
试题解析: (1)如图所示,
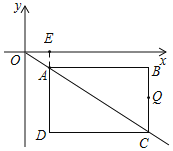
∵AB=4,AD=3,
∴A(4,3),AC=5,
过A作AE⊥x轴于E,则△AOE∽△CAB,
∴AE:OE:AO=3:4:5,
当t=2时,OA=2,OE=85,AE=65,BQ=2,
∴A(![]() ,
,![]() ),
),
∵OE+AB=![]() ,AE+BQ=
,AE+BQ=![]() ,
,
∴Q(![]() ,
,![]() ),
),
故答案为:(4,3),(![]() ,
,![]() ),(
),(![]() ,
, ![]() );
);
(2)①当点Q在BC上时,连接AQ,
∵BQ=t,BC=3,
∴CQ=3t,
∴△ACQ的面积=![]() ×CQ×AB,即S=
×CQ×AB,即S=![]() ×(3t)×4=2t+6(0t<3);
×(3t)×4=2t+6(0t<3);
②当点Q在CD上时,连接AQ,
∵QC+BC=t,BC=3,
∴CQ=t3,
∴△ACQ的面积=![]() ×CQ×AD,即S=
×CQ×AD,即S=![]() ×(t3)×3=
×(t3)×3=![]() t
t![]() (3t7);
(3t7);
∴S关于t的函数关系式为S=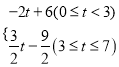 ;
;
(3)如图所示,过A作AE⊥x轴于E,则△AOE∽△CAB,
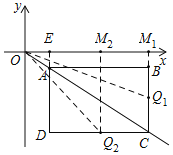
∴AE:OE:AO=3:4:5,
∵OA=t,
∴OE=![]() t,AE=
t,AE=![]() t,
t,
①当点Q在BC上时,连接OQ,
∵∠OMQ=∠D=90°,而BQ=t,
∴当![]() 时,△OMQ∽△CDA,
时,△OMQ∽△CDA,
此时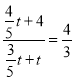 ,解得t=3;
,解得t=3;
当![]() 时,△OMQ∽△ADC,
时,△OMQ∽△ADC,
此时, 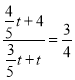 ,解得t=10>3,(舍去);
,解得t=10>3,(舍去);
②当点Q在CD上时,连接OQ,而DQ=3+4t=7t=EM,
∴OM=![]() t+7t=7
t+7t=7![]() t,
t,
∴当![]() 时,△OMQ∽△CDA,
时,△OMQ∽△CDA,
此时, 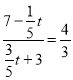 ,解得t=3;
,解得t=3;
当![]() 时,△OMQ∽△ADC,
时,△OMQ∽△ADC,
此时, 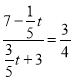 解得t=
解得t=![]() >7,(舍去)
>7,(舍去)
综上所述,当△QMO与△ACD相似时,t的值为3秒。

 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案