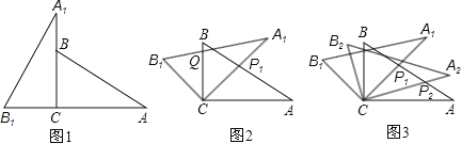
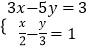题目内容
【题目】如图,以△ABC的三边为边在BC的同侧分别作三个等边三角形,即△ABD、△BCE、△ACF,当△ABC满足什么条件时,四边形ADEF是菱形?( ) 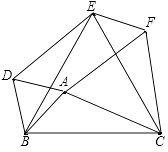
A.AB=AC
B.∠BAC=90°
C.∠BAC=120°
D.∠BAC=150°
【答案】A
【解析】解:∵△ABD和△BCE是等边三角形, ∴BD=AB,BE=BC,∠DBA=∠EBC=60°,
∴∠DBE=∠CBA=60°﹣∠EBA,
在△DBE和△ABC中, ,
,
∴△DBE≌△ABC(SAS),
∴DE=AC,
∵△AFC是等边三角形,
∴AF=AC,
∴AF=DE,
同理AD=EF,
∴四边形ADEF是平行四边形,
当AB=AC时,∵AD=AB,AC=AF,
∴AD=AF,
∴四边形ADEF是菱形,
故选A.
【考点精析】本题主要考查了菱形的判定方法的相关知识点,需要掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形才能正确解答此题.

练习册系列答案
相关题目