题目内容
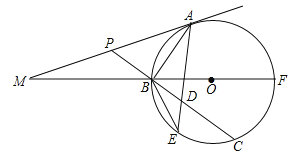
【题目】如图所示,已知![]() 的直径
的直径![]() ,弦
,弦![]() ,
,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)求![]() 的长.
的长.
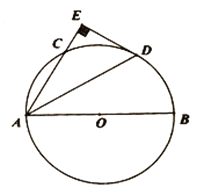
【答案】(1)证明见解析;(2)DE=4.
【解析】
(1)连接OD,欲证明![]() 是
是![]() 的切线,只要证明
的切线,只要证明![]() 即可.
即可.
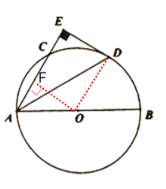
(2)过点O作![]() 于点F,只要证明四边形OFED是矩形即可得到
于点F,只要证明四边形OFED是矩形即可得到![]() ,在
,在![]() 中利用勾股定理求出OF即可.
中利用勾股定理求出OF即可.
(1)证明:连接OD
∵AD平分∠BAC,∴∠DAE=∠DAB.
∵OA=OD,∴∠ODA=∠DAO.∴∠ODA=∠DAE.∴OD∥AE.
∵DE⊥AC,∴OD⊥DE.
∴DE是⊙O切线.
(2)过点O作OF⊥AC于点F.
∴AF=CF=3.∴OF=OA2-AF2=52-32=4.
∵∠OFE=∠DEF=∠ODE=90°,
∴四边形OFED是矩形.
∴DE=OF=4.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】列方程组解应用题某校组织“大手拉小手,义卖献爱心”活动,计划购买黑、白两种颜色的文化衫进行手绘设计后出售,并将所获利润全部捐给山区困难孩子.已知该学校从批发市场花2400元购买了黑、白两种颜色的文化衫100件,每件文化衫的批发价及手绘后的零售价如表:
批发价(元) | 零售价(元) | |
黑色文化衫 | 25 | 45 |
白色文化衫 | 20 | 35 |
(1)学校购进黑、白文化衫各几件?
(2)通过手绘设计后全部售出,求该校这次义卖活动所获利润.