题目内容
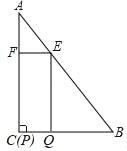
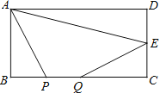
【题目】如图所示,在平行四边形![]() 中,
中,![]() 于
于![]() ,
,![]() 平分
平分![]() 交线段
交线段![]() 于
于![]() .
.
(1)如果![]() ,求证:
,求证:![]() ;
;
(2)一般的情况下,如果![]() ,试探究线段
,试探究线段![]() 、
、![]() 与
与![]() 之间的所满足的等量关系(其中
之间的所满足的等量关系(其中![]() ,
,![]() 是已知数).
是已知数).

【答案】(1)证明见解析;(2)nCD=mAF+nBE.
【解析】
(1)延长EA到G,使得![]() ,连接DG,根据四边形ABCD是平行四边形,推出
,连接DG,根据四边形ABCD是平行四边形,推出![]() ,求出
,求出![]() ,根据SAA证明
,根据SAA证明![]() ,推出
,推出![]() ,
,![]() ,求出
,求出![]() ,推出
,推出![]() 即可;
即可;
(2)延长EA到G,使得![]() ,连接DG,根据两边对应成比例,且夹角相等,两三角形相似,推出
,连接DG,根据两边对应成比例,且夹角相等,两三角形相似,推出![]() ,推出
,推出![]() ,代入即可求出答案.
,代入即可求出答案.
(1)过D作DH⊥BC的延长线于H点,并截取HG=AF,连接DG

∵四边形ABCD是平行四边形
∴![]()
∵![]() 于点E
于点E
∴![]()
∴![]()
∴![]()
在△ABE和△DGA中

∴![]()
∴![]()
∵四边形ABCD是平行四边形
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴![]()
(2)nCD = mAF + nBE.
理由是:延长EA到G,使得![]() ,连接DG,
,连接DG,

即![]()
因为四边形ABCD是平行四边形
所以AB=CD,![]() ,AD=BC,
,AD=BC,
因为![]() 于点E
于点E
所以∠AEB=∠AEC=90°
所以∠AEB=∠DAG=90°
所以∠DAG=90°,
即∠AEB=∠GAD=90°
因为![]()
所以![]()
所以∠1=∠2,![]() ,
,
所以∠GFD=90°-∠3
因为DF平分∠ADC
所以∠3=∠4
所以∠GDF=∠2+∠3=∠1+∠4=180°-∠FAD-∠3=90°-∠3
所以∠GDF=∠GFD
所以DG=GF
因为![]() ,AB=CD(已证)
,AB=CD(已证)
所以nCD=mDG=m ![]()
即nCD= mAF + nBE.

【题目】某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示:
时间x(天) | 1≤x≤7 | 8≤x≤14 |
售价(元/斤) | 第1次降价后的价格 | 第2次降价后的价格 |
销量(斤) | 80﹣3x | 120﹣x |
储存和损耗费用(元) | 40+3x | 3x2﹣64x+400 |
已知该种水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1≤x≤14)之间的函数关系式,并求出第几天时销售利润最大?