题目内容
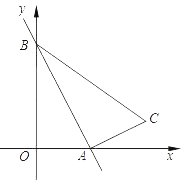
【题目】如图在以点O为原点的数轴上,点A表示的数是3,点B在原点的左侧,且AB=6AO(我们把数轴上两点之间的距离用表示两点的大写字母一起标记,比如,点A与点B之间的距离记作AB).
(1)B点表示的数是_______.
(2)若动点P从O点出发,以每秒2个单位长度的速度匀速向左运动,问经过几秒钟后PA=3PB?并求出此时P点在数轴上对应的数.
(3)若动点M.P.N分别同时从A、O、B出发,匀速向右运动,其速度分别为1个单位长度/秒.2个单位长度/秒.4个单位长度/秒,设运动时间为t秒,请直接写出PM.PN.MN中任意两个相等时的时间.
![]()
【答案】(1)-15;(2)点P运动5.25秒,此时点P表示的数是-10.5或点P运动12秒,此时点P表示的数是-24;(3)当PM=PN时,t=12;当PM=MN时,t=7.5;当PN=MN时,t=3
【解析】
(1)A、B两点在原点两侧,则AB=OA+OB,知点A表示的数即OA 的长度,利用AB=6OA求出AB, 再用AB-OA即可求得OB的长,得到点B所表示的数
(2)点P由点O向左运动,可以在OB之间,也可以在点B左侧,所以应分两种情况;
(3)此问可理解为行程问题中的追及问题,两个点在运动t秒后的路程差为开始时的距离,依次即可解题.
解:(1)由题意得OA=3,OA+OB=AB
∵AB=6OA
∴AB=6![]()
∴OB=AB-OA=18-3=15
∴点B表示的数是![]()
(2)设点P运动x秒,分两种情况:
①当点P在线段OB上时
∵PA=3PB
∴2x+3=3(15-2x)
x=5.25
∴2x=10.5
即点P表示的数是-10.5
②当点P在点B左侧时,得
2x+3=3(2x-15)
x=12
∴2x=24
即点P表示的数是-24.
综上,点P运动5.25秒,此时点P表示的数是-10.5或点P运动12秒,此时点P表示的数是-24.
(3)运动t秒后,PM=3+t-2t=3-t,PN=15+2t-4t=15-2t,MN=18+t-4t=18-3t
当PM=PN时,3-t=15-2t得t=12
当PM=MN时,3-t=18-3t得t=7.5
当PN=MN时,15-2t=18-3t,得t=3

【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎,该打车方式的总费用由里程费和耗时费组成,其中里程费按x元/公里计算,耗时费按y元/分钟计算(总费用不足9元按9元计价).小明、小刚两人用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与打车时间如表:
时间(分钟) | 里程数(公里) | 车费(元) | |
小明 | 8 | 8 | 12 |
小刚 | 12 | 10 | 16 |
(1)求x,y的值;
(2)如果小华也用该打车方式,打车行驶了11公里,用了14分钟,那么小华的打车总费用为多少?