题目内容
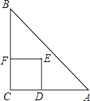
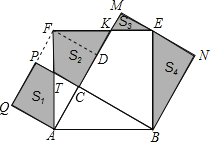
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4.分别以AB,AC,BC为边在AB的同侧作正方形ABEF,ACPQ,BCMN,四块阴影部分的面积分别为S1,S2,S3,S4,则S1+S2+S3+S4等于____.

【答案】18
【解析】
过F作AM的垂线交AM于D,连接FP,通过证明△ADF≌△BCA,△DFK≌△CAT,得出S2=S△ABC;证明△FPT≌△EMK,可得出S1+S3=S△AQF=S△ABC;证明△ABC≌△EBN,得出S4=S△ABC,进而即可求解.
解:过F作AM的垂线交AM于D,连接FP,则
∠FDA=∠DAQ=∠Q=90°,∴四边形ADFQ为矩形,∴∠PFD=90°,∴∠FPC=90°,
∴点F,P,Q在同一直线上.
∵四边形ABEF为正方形,
∴AB=AF,∠FAB=90°=∠FAD+∠CAB,
又∠ACB=90°,∴∠CAB+∠ABC=90°,
∴∠FAD=∠ABC,
又∠ACB=∠ADF=90°
∴△ADF≌△BCA(AAS)①,
∴DF=AC,同理可得△DFK≌△CAT,
∴S2=S△ADF=S△ABC.
由△DFK≌△CAT,∴FK=AT,∠DKF=∠CTA,
∴KE=FT,∠EKM=∠FTP,又∠M=∠FPT=90°,
∴△FPT≌△EMK(AAS),
∴S3=S△FPT,
又四边形ADFQ为矩形,∴S△AQF=S△ADF =S△ACB,
∴S1+S3=S△AQF=S△ABC.
同①可证明△ABC≌△EBN,
∴S4=S△ABC,
∴S1+S2+S3+S4=(S1+S3)+S2+S4=S△ABC+S△ABC+S△ABC=6+6+6=18,
故答案为:18.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目