题目内容
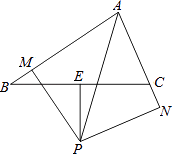
【题目】如图,∠ABD,∠ACD的角平分线交于点P,若∠A=50°,∠D=10°,求∠P的度数.

【答案】∠P=20°.
【解析】
延长PC交BD于E,设AC、PB交于F,根据三角形的内角和定理得到∠A+∠ABF+∠AFB=∠P+∠PCF+∠PFC=180°推出∠P+∠PCF=∠A+∠ABF,根据三角形的外角性质得到∠P+∠PBE=∠PED,推出∠P+∠PBE=∠PCD-∠D,根据PB、PC是角平分线得到∠PCF=∠PCD,∠ABF=∠PBE,推出2∠P=∠A-∠D,代入即可求出∠P.
解:延长PC交BD于E,设AC、PB交于F,
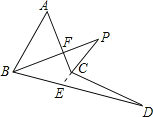
∵∠A+∠ABF+∠AFB=∠P+∠PCF+∠PFC=180°,
∵∠AFB=∠PFC,
∴∠P+∠PCF=∠A+∠ABF,
∵∠P+∠PBE=∠PED,∠PED=∠PCD﹣∠D,
∴∠P+∠PBE=∠PCD﹣∠D,
∴2∠P+∠PCF+∠PBE=∠A﹣∠D+∠ABF+∠PCD,
∵PB、PC是角平分线
∴∠PCF=∠PCD,∠ABF=∠PBE,
∴2∠P=∠A﹣∠D
∵∠A=50°,∠D=10°,
∴∠P=20°.
故答案为:∠P=20°.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目