МвДҝДЪИЭ
ЎҫМвДҝЎҝОдәәДіОД»ҜВГУО№«ЛҫОӘБЛФЪҫьФЛ»бЖЪјдёьәГөШРыҙ«ОдәәЈ¬ФЪ№Өі§¶ЁЦЖБЛТ»ЕъҫЯУРЕЁУфөДОдәәМШЙ«өДЙМЖ·Ј®ОӘБЛБЛҪвКРіЎЗйҝцЈ¬ёГ№«ЛҫПтКРіЎН¶·Е![]() Ј¬
Ј¬![]() РНЙМЖ·№І
РНЙМЖ·№І![]() јюҪшРРКФПъЈ¬
јюҪшРРКФПъЈ¬![]() РНЙМЖ·іЙұҫјЫ
РНЙМЖ·іЙұҫјЫ![]() ФӘ/јюЈ¬
ФӘ/јюЈ¬![]() ЙМЖ·іЙұҫјЫ
ЙМЖ·іЙұҫјЫ![]() ФӘ/јюЈ¬ЖдЦР
ФӘ/јюЈ¬ЖдЦР![]() РНЙМЖ·өДјюКэІ»ҙуУЪ
РНЙМЖ·өДјюКэІ»ҙуУЪ![]() РНөДјюКэЈ¬ЗТІ»РЎУЪ
РНөДјюКэЈ¬ЗТІ»РЎУЪ![]() јюЈ¬ТСЦӘ
јюЈ¬ТСЦӘ![]() РНЙМЖ·өДКЫјЫОӘ
РНЙМЖ·өДКЫјЫОӘ![]() ФӘЈҜјюЈ¬
ФӘЈҜјюЈ¬![]() РНЙМЖ·өДКЫјЫОӘ
РНЙМЖ·өДКЫјЫОӘ![]() ФӘЈҜјюЈ¬ЗТИ«ІҝКЫіцЈ®ЙиН¶·Е
ФӘЈҜјюЈ¬ЗТИ«ІҝКЫіцЈ®ЙиН¶·Е![]() РНЙМЖ·
РНЙМЖ·![]() јюЈ¬ёГ№«ЛҫПъКЫХвЕъЙМЖ·өДАыИу
јюЈ¬ёГ№«ЛҫПъКЫХвЕъЙМЖ·өДАыИу![]() ФӘЈ®
ФӘЈ®
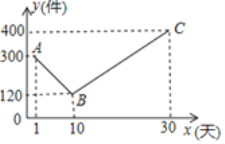
ЈЁ1Ј©ЦұҪУРҙіц![]() Ул
Ул![]() Ц®јдөДәҜКэ№ШПөКҪЈә_______Ј»
Ц®јдөДәҜКэ№ШПөКҪЈә_______Ј»
ЈЁ2Ј©ОӘБЛК№ХвЕъЙМЖ·өДАыИуЧоҙуЈ¬ёГ№«ЛҫУҰёГПтКРіЎН¶·Е¶аЙЩјю![]() РНЙМЖ·ЈҝЧоҙуАыИуКЗ¶аЙЩЈҝ
РНЙМЖ·ЈҝЧоҙуАыИуКЗ¶аЙЩЈҝ
ЈЁ3Ј©ёГ№«Лҫҫц¶ЁФЪКФПъ»о¶ҜЦРГҝКЫіцТ»јю![]() РНЙМЖ·Ј¬ҫНҙУТ»јю
РНЙМЖ·Ј¬ҫНҙУТ»јю![]() РНЙМЖ·өДАыИуЦРҫиПЧҙИЙЖЧКҪр
РНЙМЖ·өДАыИуЦРҫиПЧҙИЙЖЧКҪр![]() ФӘЈ¬өұёГ№«ЛҫКЫНкХв
ФӘЈ¬өұёГ№«ЛҫКЫНкХв![]() јюЙМЖ·ІўҫиПЧЧКҪрәу»сөГөДЧоҙуКХТжОӘ
јюЙМЖ·ІўҫиПЧЧКҪрәу»сөГөДЧоҙуКХТжОӘ![]() ФӘКұЈ¬Зу
ФӘКұЈ¬Зу![]() өДЦөЈ®
өДЦөЈ®
Ўҫҙр°ёЎҝЈЁ1Ј©![]() Ј»ЈЁ2Ј©УҰН¶·Е
Ј»ЈЁ2Ј©УҰН¶·Е![]() јю
јю![]() Ј¬ЧоҙуАыИуОӘ
Ј¬ЧоҙуАыИуОӘ![]() ФӘЈ»ЈЁ3Ј©ВъЧгМхјюКұ
ФӘЈ»ЈЁ3Ј©ВъЧгМхјюКұ![]() өДЦөОӘ
өДЦөОӘ![]()
ЎҫҪвОцЎҝ
ЈЁ1Ј©ёщҫЭАыИу=ЈЁКЫјЫ-іЙұҫЈ©![]() КэБҝјҙҝЙЗуіц
КэБҝјҙҝЙЗуіц![]() Ул
Ул![]() Ц®јдөДәҜКэ№ШПөКҪ.
Ц®јдөДәҜКэ№ШПөКҪ.
ЈЁ2Ј©yУл![]() Ц®јдКЗТ»ҙОәҜКэ№ШПөКҪЈ¬ёщҫЭТ»ҙОәҜКэөДРФЦКҝЙЦӘөұx=125КұyУРЧоҙуЦөЈ»
Ц®јдКЗТ»ҙОәҜКэ№ШПөКҪЈ¬ёщҫЭТ»ҙОәҜКэөДРФЦКҝЙЦӘөұx=125КұyУРЧоҙуЦөЈ»
ЈЁ3Ј©ҫиПЧЧКҪрәу»сөГөДКХТжОӘ![]()
![]() Ј»өұ
Ј»өұ![]() Кұ
Кұ![]() Кұ
Кұ![]() УРЧоҙуЦө18000Ј¬јҙҝЙЗуіцaЦө.
УРЧоҙуЦө18000Ј¬јҙҝЙЗуіцaЦө.
ЈЁ1Ј©![]()
ЈЁ2Ј©УЙМвТвҝЙЦӘ![]() Ј¬јҙ
Ј¬јҙ![]()
УЙТ»ҙОәҜКэөДРФЦКҝЙЦӘЈ®![]() ФҪҙуЈ¬
ФҪҙуЈ¬![]() ФҪҙу
ФҪҙу
өұ![]() Кұ
Кұ ![]()
ЎаУҰН¶·Е![]() јю
јю![]() Ј¬ЧоҙуАыИуОӘ
Ј¬ЧоҙуАыИуОӘ![]() ФӘЈ®
ФӘЈ®
ЈЁ3Ј©Т»№Іҫиіц![]() ФӘ
ФӘ
Ўа![]()
![]()
Ўаөұ![]() Кұ
Кұ![]() ЧоҙуЦөРЎУЪ
ЧоҙуЦөРЎУЪ![]()
өұ![]() Кұ
Кұ![]() Кұ
Кұ![]() УРЧоҙуЦөЈ®
УРЧоҙуЦөЈ®
јҙ![]()
Ўа![]()
јҙВъЧгМхјюКұ![]() өДЦөОӘ
өДЦөОӘ![]() .
.

 ГыРЈҝОМГПөБРҙр°ё
ГыРЈҝОМГПөБРҙр°ёЎҫМвДҝЎҝДіРЈОӘБЛәлСпЦР»Әҙ«НіОД»ҜЈ¬БЛҪвС§ЙъХыМеФД¶БДЬБҰЈ¬ЧйЦҜИ«РЈөД1000ГыС§ЙъҪшРРТ»ҙОФД¶БАнҪвҙуИьЈ®ҙУЦРійИЎІҝ·ЦС§ЙъөДіЙјЁҪшРРНіјЖ·ЦОцЈ¬ёщҫЭІвКФіЙјЁ»жЦЖБЛЖөКэ·ЦІјұнәНЖөКэ·ЦІјЦұ·ҪНјЈә
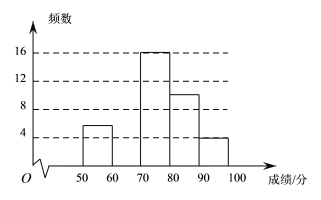
·ЦЧй/·Ц | ЖөКэ | ЖөВК |
50ЎЬxЈј60 | 6 | 0.12 |
60ЎЬxЈј70 |
| 0.28 |
70ЎЬxЈј80 | 16 | 0.32 |
80ЎЬxЈј90 | 10 | 0.20 |
90ЎЬxЎЬ100 | 4 | 0.08 |
ЈЁ1Ј©ЖөКэ·ЦІјұнЦРөД![]() Ј»
Ј»
ЈЁ2Ј©Ҫ«ЙПГжөДЖөКэ·ЦІјЦұ·ҪНјІ№ідНкХыЈ»
ЈЁ3Ј©Из№ыіЙјЁҙпөҪ90ј°90·ЦТФЙПХЯОӘУЕРгЈ¬ҝЙНЖјцІОјУҫцИьЈ¬№АјЖёГРЈҪшИлҫцИьөДС§ЙъҙуФјУР ИЛЈ®