题目内容
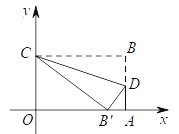
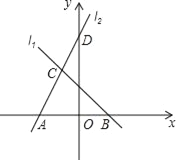
【题目】如图，直线l1的解析式为y=﹣x+2，l1与x轴交于点B，直线l2经过点D（0，5），与直线l1交于点C（﹣1，m），且与x轴交于点A,
（1）求点C的坐标及直线l2的解析式；
（2）求△ABC的面积．
【答案】（1）C（﹣1，3），直线l2的解析式为y=2x+5；（2）△ABC的面积为
．
【解析】
试题（1）由题意把点C(－1，m)的坐标代入y=－x+2即可求得m的值，再结合直线l2经过点D(0，5)即可根据待定系数法求得直线l2的解析式；
（2）先分别求得两条直线与x轴的交点坐标，再根据三角形的面积公式即可求得结果.
（1）在y=－x+2中，当
时，
∴点C的坐标为（－1，3）
设直线l2的解析式为
∵图象过点C（－1，3），D（0，5）
∴
，解得
∴直线l2的解析式为
；
（1）在y=－x+2中，当
时，
，
，即A点坐标为（2，0）
在中，当时，
，
，即A点坐标为（
，0）
∴
练习册系列答案
相关题目
【题目】某工厂一周计划每日生产自行车100辆，由于工人实行轮休，每日上班人数不一定相等，实际每日生产量与计划量相比情况如下表（以计划量为标准，增加的车辆数记为正数，减少的车辆数记为负数）:
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减（辆） | －1 | +3 | －2 | －4 | +7 | －5 | －10 |
（1）生产量最多的一天比生产量最少的一天多生产多少辆？
（2）本周总的生产量是多少辆？
