题目内容
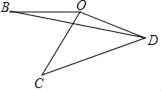
【题目】将线段OB绕点O逆时针旋转60°得到线段OC,继续旋转α(0°<α<120°)得到线段OD,连接CD.
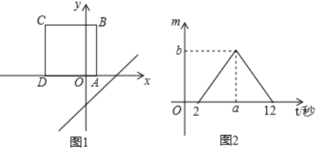
(1)如图,连接BD,则∠BDC的大小=_____(度);
(2)将线段OB放在平面直角坐标系中,O是坐标原点,点B的坐标为(﹣6,0),以OB为斜边作Rt△OBE,使∠OBE=∠OCD,且点E在第三象限,若∠CED=90°,则α的大小=_____(度),点D的坐标为_____.
【答案】 30 90 (3![]() ,﹣3)
,﹣3)
【解析】分析:(1)根据图形旋转的性质可知OB=OC=OD,再由圆周角定理即可得出结论;
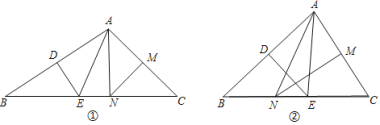
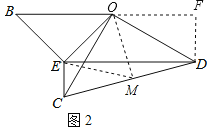
(2)如图2,过点O作OM⊥CD于点M,连接EM,先根据AAS定理得出△OEB≌△OMC,故可得出OE=OM,∠BOE=∠COM,所以△OEM是等边三角形.根据OC=OD,OM⊥CD可知CM=DM.故可得出点O、C、D在以M为圆心,MC为半径的圆上.由圆周角定理可得α的大小,再根据三角函数得出结论.
详解:(1)∵线段OC,OD由OB旋转而成,
∴OB=OC=OD.
∴点B、C、D在以O为圆心,AB为半径的圆上.
∴∠BDC=![]() ∠BOC=30°.
∠BOC=30°.
(2)如图2,过点O作OM⊥CD于点M,连接EM,过点D作BF⊥BO的延长线于点F.
∵∠OMD=90°,
∴∠OMC=90°.
在△OEB与△OMC中,
 ,
,
∴△OEB≌△OMC.
∴OE=OM,∠BOE=∠COM.
∴∠EOM=∠EOC+∠COM=∠EOC+∠BOE=∠BOC=60°.
∴△OEM是等边三角形.
∴EM=OM=OE.
∵OC=OD,OM⊥CD,
∴CM=DM.
又∵∠DEC=90°,
∴EM=CM=DM.
∴OM=CM=DM.
∴点O、C、D、E在以M为圆心,MC为半径的圆上.
∴α=∠COD=90°,
∴∠FOD=30°,
∴OF=3![]() ,DF=3,
,DF=3,
∴点D的坐标为(3![]() ,-3).
,-3).

 阅读快车系列答案
阅读快车系列答案