题目内容
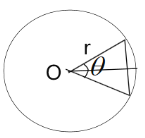
【题目】如图,利用我们现在已经学过的圆和锐角三角函数的知识可知,半径 r 和圆心角θ及其所对的弦长 l之间的关系为![]() ,从而
,从而![]()
![]() ,综合上述材料当
,综合上述材料当![]() 时,
时,![]() ______.
______.
【答案】![]()
【解析】
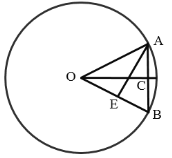
如图所示,∠AOB=θ,OA=r,AB=l,∠AOC=∠BOC=![]() ,根据
,根据![]() ,设AB=l=2a,OA =r=3a,根据等量代换得出∠BOC=∠BAE=
,设AB=l=2a,OA =r=3a,根据等量代换得出∠BOC=∠BAE=![]() ,求出BE,利用勾股定理求出AE,即可表达出
,求出BE,利用勾股定理求出AE,即可表达出![]() ,代入计算即可.
,代入计算即可.
解:如图所示,∠AOB=θ,OA=r,AB=l,∠AOC=∠BOC=![]() ,
,
∵AO=BO,
∴OC⊥AB,
∴![]() ,
,
∴设AB=l=2a,OA =r=3a,
过点A作AE⊥OB于点E,
∵∠B+∠BOC=90°,∠B+∠BAE=90°,
∴∠BOC=∠BAE=![]() ,
,
∴![]() ,即
,即![]() ,解得:
,解得:![]() ,
,
由勾股定理得:![]() ,
,
∴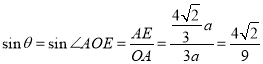 ,
,
故答案为:![]() .
.

练习册系列答案
相关题目