题目内容
如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,已知AD=AB=3,BC=4,动点P从B点出发,沿线段BC向点C作匀速运动:动点Q从点D出发,沿线段DA向点A作匀速运动.过Q点垂直于AD的射线交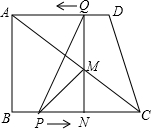 AC于点M,交BC于点N.P、Q两点同时出发,速度都为每秒1个单位长度.当Q点运动到A点,P、Q两点同时停止运动.设点Q运动的时问为t秒.
AC于点M,交BC于点N.P、Q两点同时出发,速度都为每秒1个单位长度.当Q点运动到A点,P、Q两点同时停止运动.设点Q运动的时问为t秒.(1)NC=
(2)当t为何值时,四边形PCDQ构成平行四边形?
(3)若△PMC为等腰三角形,求t的值.
分析:(1)依据题意易知四边形ABNQ是矩形∴NC=BC-BN=BC-AQ=BC-AD+DQ,BC、AD已知,DQ就是t,即解;∵AB∥QN,∴△CMN∽△CAB,∴CM:CA=CN:CB,CB、CN已知,根据勾股定理可求CA=5,即可表示CM;
(2)四边形PCDQ构成平行四边形就是PC=DQ,列方程4-t=t即解;
(3)由于等腰三角形的两腰不确定,因此分三种情况进行讨论:
①当MP=MC时,那么PC=2NC,据此可求出t的值.
②当CM=CP时,可根据CM和CP的表达式以及题设的等量关系来求出t的值.
③当MP=PC时,在直角三角形MNP中,先用t表示出三边的长,然后根据勾股定理即可得出t的值.
综上所述可得出符合条件的t的值.
(2)四边形PCDQ构成平行四边形就是PC=DQ,列方程4-t=t即解;
(3)由于等腰三角形的两腰不确定,因此分三种情况进行讨论:
①当MP=MC时,那么PC=2NC,据此可求出t的值.
②当CM=CP时,可根据CM和CP的表达式以及题设的等量关系来求出t的值.
③当MP=PC时,在直角三角形MNP中,先用t表示出三边的长,然后根据勾股定理即可得出t的值.
综上所述可得出符合条件的t的值.
解答:解:(1)∵AQ=3-t
∴CN=4-(3-t)=1+t,
在Rt△ABC中,AC2=AB2+BC2=32+42
∴AC=5,
在Rt△MNC中,cos∠NCM=
=
,CM=
.
(2)由于四边形PCDQ构成平行四边形,
∴PC=QD,即4-t=t
解得t=2.
(3)①当MP=MC时(如图)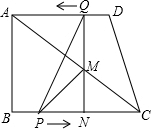
则有:NP=NC
即PC=2NC∴4-t=2(1+t)
解得:t=
②当CM=CP时(如图)
则有:
(1+t)=4-t
解得:t=
③当PM=PC时(如图)
在Rt△MNP中,PM2=MN2+PN2
而MN=
NC=
(1+t),PN=PC-NC=(4-t)-(1+t)=3-2t,
∴[
(1+t)]2+(3-2t)2=(4-t)2,
解得:t1=
,t2=-1(舍去)
∴当t=
,t=
,t=
时,△PMC为等腰三角形.
∴CN=4-(3-t)=1+t,
在Rt△ABC中,AC2=AB2+BC2=32+42
∴AC=5,
在Rt△MNC中,cos∠NCM=
| NC |
| MC |
| 4 |
| 5 |
| 5+5t |
| 4 |
(2)由于四边形PCDQ构成平行四边形,
∴PC=QD,即4-t=t
解得t=2.
(3)①当MP=MC时(如图)

则有:NP=NC
即PC=2NC∴4-t=2(1+t)
解得:t=
| 2 |
| 3 |
②当CM=CP时(如图)
则有:
| 5 |
| 4 |
解得:t=
| 11 |
| 9 |
③当PM=PC时(如图)
在Rt△MNP中,PM2=MN2+PN2
而MN=
| 3 |
| 4 |
| 3 |
| 4 |
∴[
| 3 |
| 4 |
解得:t1=
| 103 |
| 57 |
∴当t=
| 2 |
| 3 |
| 11 |
| 9 |
| 103 |
| 57 |
点评:本题考查平行四边形性质及等腰三角形性质以及数学的动点问题和三角函数的运用.考查学生分类讨论和数形结合的数学思想方法.

练习册系列答案
相关题目
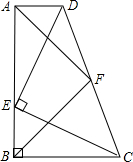 如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,点E是AB边上一点,AE=BC,DE⊥EC,取DC的中点F,连接AF、BF.
如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,点E是AB边上一点,AE=BC,DE⊥EC,取DC的中点F,连接AF、BF.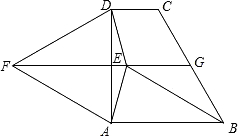 ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.
ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.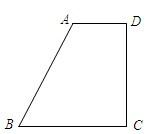 如图,直角梯形ABCD中,AD∥BC,∠BCD=90°,且CD=2AD,tan∠ABC=2.
如图,直角梯形ABCD中,AD∥BC,∠BCD=90°,且CD=2AD,tan∠ABC=2.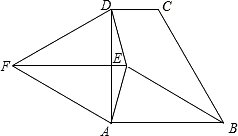 (2013•深圳二模)如图,直角梯形ABCD中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60°.以AD为边在直角梯形ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.
(2013•深圳二模)如图,直角梯形ABCD中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60°.以AD为边在直角梯形ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF. 已知:如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,以AB为直径的⊙O切DC边于E点,AD=3cm,BC=5cm.求⊙O的面积.
已知:如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,以AB为直径的⊙O切DC边于E点,AD=3cm,BC=5cm.求⊙O的面积.