题目内容
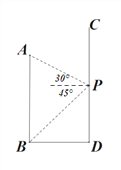
【题目】如图，AB、CD分别表示两幢相距36米的大楼，小明同学站在CD大楼的P处窗口观察AB大楼的底部B点的俯角为45°，观察AB大楼的顶部A点的仰角为30°.
（1）求PD的高；
（2）求大楼AB的高．
【答案】（1）PD的高为36米（2）大楼AB的高为（
）米
【解析】试题分析：过点P作AB的垂线，垂足为E，根据题意可得出四边形PDBE是矩形，再由∠EPB=45°可知BE=PE=36m，由AE=PEtan30°得出AE的长，进而可得出结论．
试题解析：如图，过点P作AB的垂线，垂足为E，
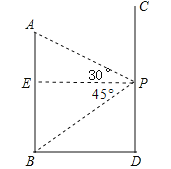
∵PD⊥AB，DB⊥AB，
∴四边形PDBE是矩形，
∵BD=36m，∠EPB=45°，
∴BE=PE=36m，
即PD=36m
∴AE=PEtan30°=36×
=12
（m），
∴AB=12+36（m）．
答：建筑物AB的高为36+12米．
练习册系列答案
相关题目
