题目内容
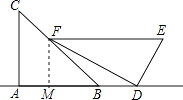
【题目】小明是一位善于思考的学生,在一次数学活动课上,他将一副直角三角板按如图所示的位置摆放,A、B、D三点在同一直线上,EF∥AD,∠CAB=∠EDF=90°,∠C=45°,∠E=60°,量得DE=8. 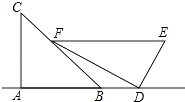
(1)试求点F到AD的距离.
(2)试求BD的长.
【答案】
(1)解:如图,过点F作FM⊥AD于点M,
在△EDF中,∠EDF=90°,∠E=60°,DE=8,
则∠DFE=30°,
故EF=2DE=16,
DF= ![]() =
= ![]() =8
=8 ![]() ,
,
∵AB∥EF,
∴∠FDM=∠DFE=30°,
在Rt△FMD中,MF= ![]() DF=8
DF=8 ![]() ×
× ![]() =4
=4 ![]() ,
,
即点F与AD之间的距离为:4 ![]()
(2)解:在Rt△FMD中,DM= ![]() =
= ![]() =12,
=12,
∵∠C=45°,∠CAB=90°,
∴∠CBA=45°,
又∵∠FMB=90°,
△FMB是等腰直角三角形,
∴MB=FM=4 ![]() ,
,
∴BD=MD﹣FM=12﹣4 ![]()
【解析】(1)根据题意得出∠DFE=30°,则EF=2DE=16,进而利用勾股定理得出DF的长,进而得出答案;(2)直接利用勾股定理得出DM的长,进而得出MB=FM,求出答案.
【考点精析】根据题目的已知条件,利用平行线的性质和勾股定理的概念的相关知识可以得到问题的答案,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

练习册系列答案
相关题目