题目内容
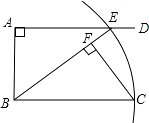
【题目】如图,AD∥BC,∠BAD=90°,以点B为圆心,BC长为半径画弧,与射线AD相交于点E,连接BE,过C点作CF⊥BE,垂足为F.线段BF与图中现有的哪一条线段相等?先将你猜想出的结论填写在下面的横线上,然后再加以证明. 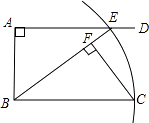
(1)结论:BF= .
(2)证明.
【答案】
(1)AE
(2)证明:∵CF⊥BE,
∴∠BFC=90°,
又∵AD∥BC,
∴∠AEB=∠FBC;
由于以点B为圆心,BC长为半径画弧,
∴BE=BC,
在△ABE与△FCB中, 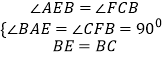
∴△ABE≌△FCB(AAS),
∴BF=AE.
【解析】解:(1)结论:BF=AE.
由题意可得BE=BC,∠AEB=∠FBC,易证明得直角三角形ABE与直角三角形FCB全等,即可得BE=AE.

练习册系列答案
相关题目