题目内容
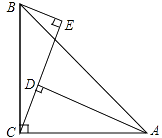
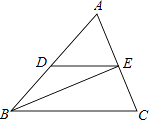
【题目】如图,已知DE∥BC,BE平分∠ABC,∠C=65°,∠ABC=50°. 
(1)求∠BED的度数;
(2)判断BE与AC的位置关系,并说明理由.
【答案】
(1)解:∵BE平分∠ABC,且∠ABC=50°,
∴∠EBC= ![]() ∠ABC=25°.
∠ABC=25°.
∵DE∥BC,
∴∠BED=∠EBC=25°.
(2)解:BE⊥AC,其理由是:
∵DE∥BC,且∠C=65°,
∴∠AED=∠C=65°.
∵∠BED=25°,
∴∠AEB=∠AED+∠BED=65°+25°=90°,
∴BE⊥AC.
【解析】(1)根据BE平分∠ABC,且∠ABC=50°,可得∠EBC= ![]() ∠ABC=25°.再根据DE∥BC,即可得出∠BED=∠EBC=25°. (2)根据DE∥BC,且∠C=65°,即可得到∠AED=∠C=65°,再根据∠BED=25°,可得∠AEB=∠AED+∠BED=65°+25°=90°,据此可得BE⊥AC.
∠ABC=25°.再根据DE∥BC,即可得出∠BED=∠EBC=25°. (2)根据DE∥BC,且∠C=65°,即可得到∠AED=∠C=65°,再根据∠BED=25°,可得∠AEB=∠AED+∠BED=65°+25°=90°,据此可得BE⊥AC.
【考点精析】关于本题考查的角的平分线和垂线的性质,需要了解从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短才能得出正确答案.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目