题目内容
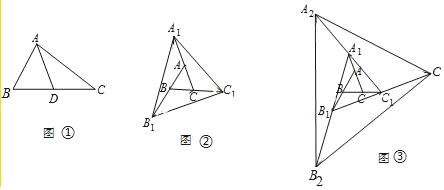
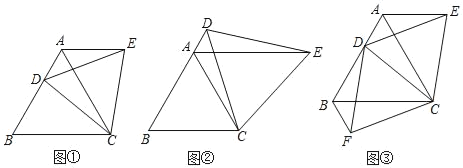
【题目】(1)操作发现:如图①,点D是等边△ABC的边AB上一动点(点D与点B不重合),连接CD,以CD为边在CD上方作等边△CDE,连接AE,则AE与BD有怎样的数量关系?说明理由.
(2)类比猜想:如图②,若点D是等边△ABC的边BA延长线上一动点,连接CD,以CD为边在CD上方作等边△CDE,连接AE,请直接写出AE与BD满足的数量关系,不必说明理由;
(3)深入探究:如图③,点D是等边△ABC的边AB上一动点(点D与点B不重合),连接CD,以CD为边分别在CD上方、下方作等边△CDE和等边△CDF,连接AE,BF则AE,BF与AB有怎样的数量关系?说明理由.
【答案】(1)AE=BD;(2)AE=BD;(3)AE+BF=AB.
【解析】
(1)根据等边三角形的三条边、三个内角都相等的性质,利用全等三角形的判定定理SAS可以证得△BCD≌△ACE;然后由全等三角形的对应边相等知AE=BD
(2)通过证明△BCD≌△ACE,即可证明AE=BD;
(3)1.AF+BF=AB;利用全等三角形△BCD≌△ACE(SAS)的对应边BD=AE;同理△BCF≌△DCA (SAS),则BF=AD,所以AE+BF =AB
解:(1)AE=BD,理由如下:
∵△ABC和△DCE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB﹣∠ACD=∠DCE﹣∠ACD,
即∠BCD=∠ACE,
在△BCD和△ACE中,
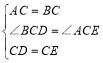 ,
,
∴△BCD≌△ACE(SAS),
∴AE=BD;
(2)AE=BD.
理由如下:∵△ABC和△DCE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠ACD=∠DCE+∠ACD,
即∠BCD=∠ACE,
在△BCD和△ACE中,
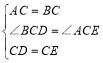 ,
,
∴△BCD≌△ACE(SAS),
∴AE=BD;
(3)AE+BF=AB.
证明如下:由(1)知,△BCD≌△ACE(SAS),
∴BD=AE,
同理可证,△BCF≌△DCA(SAS),
∴BF=AD,
∴AB=AD+BD=AE+BF.