题目内容
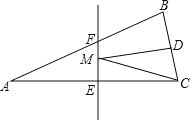
【题目】如图,两艘海监船刚好在某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍船只停在C处海域,AB=60(![]() +3)海里,在B处测得C在北偏东45°方向上,A处测得C在北偏西30°方向上,在海岸线AB上有一等他D,测得AD=100海里.
+3)海里,在B处测得C在北偏东45°方向上,A处测得C在北偏西30°方向上,在海岸线AB上有一等他D,测得AD=100海里.
(1)分别求出AC,BC(结果保留根号)
(2)已知在灯塔D周围80海里范围内有暗礁群,在A处海监船沿AC前往C处盘看,图中有无触礁的危险?请说明理由.
【答案】A与C的距离为120![]() 海里,B与C的距离为180
海里,B与C的距离为180![]() 海里;(2)无触礁危险.
海里;(2)无触礁危险.
【解析】试题分析:(1)、过点C作CE⊥AB于点E,可得∠CBD=45°,∠CAD=60°,设CE=x,根据Rt△CAE的三角函数得出AE= ![]() ,最后根据AB=BE+AE求出x的值,最后根据直角三角形的三角函数求出答案;(2)、过点D作DF⊥AC于点F,根据Rt△ADF的三角函数求出DF的长度,然后与80进行比较大小,从而得出答案.
,最后根据AB=BE+AE求出x的值,最后根据直角三角形的三角函数求出答案;(2)、过点D作DF⊥AC于点F,根据Rt△ADF的三角函数求出DF的长度,然后与80进行比较大小,从而得出答案.
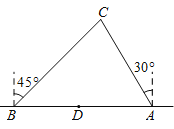
试题解析:(1)、如图所示,过点C作CE⊥AB于点E,可得∠CBD=45°,∠CAD=60°,
设CE=x,在Rt△CBE中,BE=CE=x,
在Rt△CAE中, ![]() ,即AE=CE·tan30°,∴AE=
,即AE=CE·tan30°,∴AE= ![]()
∵AB=60(![]() +3)海里,∴AB=BE+AE=x+
+3)海里,∴AB=BE+AE=x+ ![]() =60(
=60(![]() ),即x=180海里,
),即x=180海里,
则AC=![]() 海里, BC=
海里, BC=![]() x=180
x=180![]() 海里;
海里;
答:A与C的距离为120![]() 海里,B与C的距离为180
海里,B与C的距离为180![]() 海里;
海里;
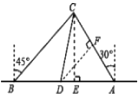
(2)、无触礁危险.
如图所示,过点D作DF⊥AC于点F,在△ADF中,∵AD=100,∠CAD=60°,∴DF=ADsin60°=50![]() ≈86.6>80,故海监船沿AC前往C处盘查,无触礁危险.
≈86.6>80,故海监船沿AC前往C处盘查,无触礁危险.

练习册系列答案
相关题目