题目内容
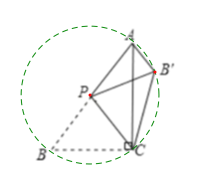
【题目】如图,在△ABC中,∠ACB=90°,AB=5,BC=3,P是AB边上的动点(不与点B重合)将△BCP沿CP所在的直线翻折,得到![]() ,连接
,连接![]() ,下面有四个判断:
,下面有四个判断:
①当AP=BP时,![]() ∥CP;
∥CP;
②当AP=BP时,![]()
③当CP⊥AB时,![]() ;
;
④![]() 长度的最小值是1.
长度的最小值是1.
所有正确结论的序号是( )
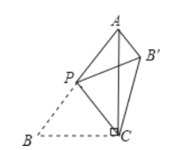
A.①③④B.①②C.①②④D.②③④
【答案】C
【解析】
①由直角三角形斜边上的中线等于斜边的一半以及折叠的性质,易得∠AB′P=∠CPB′,即可得AB′∥CP;②由PA=PB′=PC=PB,可得点A,B′,C,B在以P为圆心,PA长为半径的圆上,然后由圆周角定理,求得答案;③当CP⊥AB时,易证得△ACP∽△ABC,然后由相似三角形的对应边成比例,求得AP的长;④易得当B′在线段AC上时,AB′的长度有最小值,继而求得答案.
∵在△ABC中,∠ACB=90°,AP=BP,
∴AP=BP=CP,
由折叠的性质可得:CP=B′P,∠CPB′=∠BPC=![]() (180°∠APB′),
(180°∠APB′),
∴AP=B′P,
∴∠AB′P=′B′AP=![]() (180°∠APB′),
(180°∠APB′),
∴∠AB′P=∠CPB′,
∴AB′∥CP,故①正确;
②∵在△ABC中,∠ACB=90°,AP=BP,将△BCP沿CP所在的直线翻折,得到![]() ,
,
∴PA=PB′=PC=PB,
∴点A,B′,C,B在以P为圆心,PA长为半径的圆上,
∵∠B′PC与∠B′AC是![]() 所对的圆心角和圆周角,
所对的圆心角和圆周角,
∴∠B′PC=2∠B′AC,故②正确;
③当CP⊥AB时,∠APC=∠ACB,
∵∠PAC=∠CAB,
∴△ACP∽△ABC,
∴![]() ,
,
∵在Rt△ABC中,AC=![]() =4,
=4,
∴AP=![]() =
=![]() ,故③错误;
,故③错误;
④由轴对称的性质可知:BC=CB′=3,
∴CB′长度固定不变,
∵在 AB′C中,AB′>ACB′C,
∴当B′在线段AC上时, AB′有最小值,此时,AB′=ACB′C=43=1,故④正确.
故选C.

【题目】某学校初二和初三两个年级各有600名同学,为了科普卫生防疫知识,学校组织了一次在线知识竞赛,小宇分别从初二、初三两个年级随机抽取了40名同学的成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.
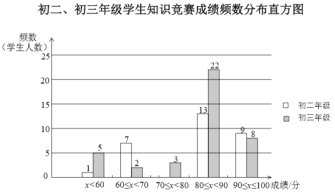
![]() .初二、初三年级学生知识竞赛成绩不完整的频数分布直方图如下(数据分成5组:
.初二、初三年级学生知识竞赛成绩不完整的频数分布直方图如下(数据分成5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ):
):
![]() .初二年级学生知识竞赛成绩在
.初二年级学生知识竞赛成绩在![]() 这一组的数据如下:
这一组的数据如下:
80 80 81 83 83 84 84 85 86 87 88 89 89
![]() .初二、初三学生知识竞赛成绩的平均数、中位数、方差如下:
.初二、初三学生知识竞赛成绩的平均数、中位数、方差如下:
平均数 | 中位数 | 方差 | |
初二年级 | 80.8 |
| 96.9 |
初三年级 | 80.6 | 86 | 153.3 |
根据以上信息,回答下列问题:
(1)补全上面的知识竞赛成绩频数分布直方图;
(2)写出表中![]() 的值;
的值;
(3)![]() 同学看到上述的信息后,说自己的成绩能在本年级排在前40%,
同学看到上述的信息后,说自己的成绩能在本年级排在前40%,![]() 同学看到
同学看到![]() 同学的成绩后说:“很遗憾,你的成绩在我们年级进不了前50%”.请判断
同学的成绩后说:“很遗憾,你的成绩在我们年级进不了前50%”.请判断![]() 同学是________(填“初二”或“初三”)年级的学生,你判断的理由是________.
同学是________(填“初二”或“初三”)年级的学生,你判断的理由是________.
(4)若成绩在85分及以上为优秀,请估计初二年级竞赛成绩优秀的人数为____.