题目内容
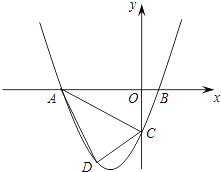
【题目】如图所示,已知函数y=ax2(a≠0)的图象上的点D,C与x轴上的点A(-5,0)和B(3,0)构成ABCD,DC与y轴的交点为E(0,6),试求a的值.
【答案】![]()
【解析】
由A(-5,0)和B(3,0)得出AB=8,进一步得出CD=AB=8,所以D点的横坐标为-4,再结合E(0,6),得出点D的纵坐标为6,代入D点坐标求得a的数值即可.
解:∵点A(-5,0)和B(3,0),
∴AB=8.
∵四边形ABCD是平行四边形,
∴CD=8,CD∥AB.
又∵AB⊥y轴,抛物线y=ax2的对称轴为y轴,∴CD⊥y轴,
∴DE=![]() CD=4,点D,C,E的纵坐标相同.
CD=4,点D,C,E的纵坐标相同.
又∵点E的坐标为(0,6),
∴点D的坐标为(-4,6).
将D(-4,6)代入y=ax2,
解得a=![]() .
.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目